题目内容
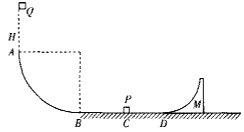
【题目】如图所示,半径为![]() 的
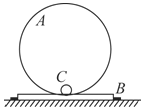
的![]() 光滑圆弧AB固定在水平面上,BCD为粗糙的水平面,BC和CD距离分别为2.5 m、1.75 m,D点右边为光滑水平面,在C点静止着一个小滑块P,P与水平面间的动摩擦因数为
光滑圆弧AB固定在水平面上,BCD为粗糙的水平面,BC和CD距离分别为2.5 m、1.75 m,D点右边为光滑水平面,在C点静止着一个小滑块P,P与水平面间的动摩擦因数为![]() ,容器M放置在光滑水平面上,M的左边是半径为
,容器M放置在光滑水平面上,M的左边是半径为![]() 的
的![]() 光滑圆弧,最左端和水平面相切于D点。一小滑块Q从A点正上方距A点高
光滑圆弧,最左端和水平面相切于D点。一小滑块Q从A点正上方距A点高![]() 处由静止释放,从A点进入圆弧并沿圆弧运动,Q与水平面间的动摩擦因数为
处由静止释放,从A点进入圆弧并沿圆弧运动,Q与水平面间的动摩擦因数为![]() 。Q运动到C点与P发生碰撞,碰撞过程没有能量损失。已知Q、P和M的质量分别为
。Q运动到C点与P发生碰撞,碰撞过程没有能量损失。已知Q、P和M的质量分别为![]() ,重力加速度
,重力加速度![]() 取
取![]() ,求:
,求:
(1)P、Q第一次碰撞后瞬间速度大小;
(2)Q经过圆弧末端B时对轨道的压力大小;
(3)M的最大速度。
【答案】(1)-8m/s 4m/s(2)43.8N(第一次)和17.8N(第二、三次)(3)5m/s
【解析】
(1)物体Q从开始下落,到到达C点的过程,由动能定理:
![]()
解得
v1=12m/s
Q运动到C点与P发生碰撞,则:
![]()
![]()
联立解得:
v2=-8m/s
v3=4m/s
(2)碰撞后Q向左滑行,设Q第二次到B点时速度为![]() ,由动能定理有
,由动能定理有
![]()
Q第二次在B点,设轨道对Q的支持力大小为![]() ,应用向心力公式有
,应用向心力公式有
![]()
解得
![]()
![]()
Q滑上圆弧轨道AB后再次滑下,第三次经过B点时的速度大小仍为![]() ,轨道对Q的支持力大小仍为
,轨道对Q的支持力大小仍为![]() ,之后Q一直向右运动,最终停在BD上,且与P无碰撞,所以由牛顿第三定律可知,Q在B点对轨道的压力大小为
,之后Q一直向右运动,最终停在BD上,且与P无碰撞,所以由牛顿第三定律可知,Q在B点对轨道的压力大小为![]() (第一次)和
(第一次)和![]() (第二、三次)
(第二、三次)
(3)P、Q碰撞后P向右滑行,设P点运动到D点速度为![]() ,由动能定理有
,由动能定理有
![]()
解得
![]()
P滑上M的轨道过程M向右加速,从轨道上滑下,M仍向右加速,则P滑到水平面时M有最大速度,设P刚到水平面时,M和P的速度分别为![]() 和
和![]() ,
,![]() 为M的最大速度,P从滑上到回到水平面,P和M水平方向动量守恒,初末两态总动能相等,则有
为M的最大速度,P从滑上到回到水平面,P和M水平方向动量守恒,初末两态总动能相等,则有
![]()
![]()
联立解得
![]()
![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目