题目内容
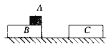
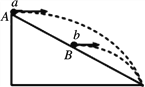
【题目】固定的倾角为37°的光滑斜面,长度L=1m,斜面顶端放置可视为质点的小物体,质量m=0.8kg,如甲图所示。当水平恒力较小时,物体可以沿斜面下滑,到达斜面底端时撤去水平恒力,物体在水平地面上滑行的距离为s。忽略物体转弯时能量损失,研究发现s与F之间的关系如乙图所示。已知g=10m/s2,sin37°=0.6,cos37°=0.8。求:
(1)乙图中斜线与横坐标轴的交点坐标值;
(2)物体在水平地面滑行过程中,产生的最大内能为多少;
(3)当F=3N时,物体在水平面上滑行的时间为多少。

【答案】(1)6 N;(2)4.8J;(3)![]() s
s
【解析】(1)当![]() 时,物体处在平衡状态。根据平衡条件:
时,物体处在平衡状态。根据平衡条件: ![]() ,解得
,解得![]()
(2)根据能量的转化关系可知,物体在水平面滑行6m时,产生的内能最大,数值为物体减少的重力势能。![]()
(3)当![]() 时,
时, ![]() ,由功能关系得:
,由功能关系得: ![]()
∴![]()
当F3=3N时,在斜面上滑行,由牛顿第二定律![]()
物块滑到斜面底端的速度![]()
![]()
水平面上物体水平方向只受摩擦力,
由牛顿第二定律![]()
因为![]()
可得![]()
所以,物体在水平面上滑动的时间为![]() 。
。

练习册系列答案
相关题目