题目内容
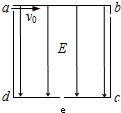 如图所示,abcd是一个正方形盒子,cd边的中点有一个小孔e.盒子中有沿ad方向的匀强电场,场强大小为E.粒子源不断地从a处的小孔沿ab方向向盒内发射相同的带电粒子,粒子的初速度为v0.在电场作用下,粒子恰好从e处的小孔射出.
如图所示,abcd是一个正方形盒子,cd边的中点有一个小孔e.盒子中有沿ad方向的匀强电场,场强大小为E.粒子源不断地从a处的小孔沿ab方向向盒内发射相同的带电粒子,粒子的初速度为v0.在电场作用下,粒子恰好从e处的小孔射出.(1)求该带电粒子从e孔射出时的速率
(2)若撤去电场,在盒中加一方向垂直于纸面的匀强磁场,使粒子仍恰好从e孔射出,求所加磁场的方向和磁感应强度的大小B.(带电粒子的重力和粒子间的相互作用力均可忽略)
分析:(1)带电粒子在匀强电场中作类平抛运动,将运动分解成水平的匀速直线运动和竖直方向的匀加速直线运动分别表示出位移与时间的关系,结合动能定理即可解得末速率.
(2)撤去电场,加上磁场带电粒子做圆周运动,粒子仍从C点离开,由左手定则可知磁场方向应垂直纸面向外,有几何知识算出圆周运动的半径,由洛仑兹力作为向心力列式解得磁感应强度的大小B.
(2)撤去电场,加上磁场带电粒子做圆周运动,粒子仍从C点离开,由左手定则可知磁场方向应垂直纸面向外,有几何知识算出圆周运动的半径,由洛仑兹力作为向心力列式解得磁感应强度的大小B.
解答:解:(1)设正方形盒子边长为L,带电粒子质量为m,电量为q,粒子从e孔射出时速率为v
带电粒子在匀强电场中做类平抛运动,
水平方向:
L=v0t①
竖直方向:L=
t2②
根据动能定理:EqL=
mv2-
m
③
由①②③解之得:v=
v0
(2)加向下的电场时,粒子向下偏,说明粒子带正电,所以撤去电场,加上磁场后,磁场方向应垂直纸面向外
加上磁场后,设圆心为O,Oe与竖直方向夹角为θ,由几何关系知
R+Rcosθ=L④
Rsinθ=
L⑤
联立①②得L=
结合④⑤R=
L
根据洛仑兹力作为向心力 qv0B=m
解之得 B=
答:(1)该带电粒子从e孔射出时的速率v=
v0
(2)若撤去电场,在盒中加一方向垂直于纸面的匀强磁场,使粒子仍恰好从e孔射出,所加磁场方向应垂直纸面向外,磁感应强度的大小B=
带电粒子在匀强电场中做类平抛运动,
水平方向:
| 1 |
| 2 |
竖直方向:L=
| 1 |
| 2 |
| Eq |
| m |
根据动能定理:EqL=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
由①②③解之得:v=
| 17 |
(2)加向下的电场时,粒子向下偏,说明粒子带正电,所以撤去电场,加上磁场后,磁场方向应垂直纸面向外
加上磁场后,设圆心为O,Oe与竖直方向夹角为θ,由几何关系知
R+Rcosθ=L④
Rsinθ=
| 1 |
| 2 |
联立①②得L=
8m
| ||
| qE |
结合④⑤R=
| 5 |
| 8 |
根据洛仑兹力作为向心力 qv0B=m
| ||
| R |
解之得 B=
| E |
| 5v0 |
答:(1)该带电粒子从e孔射出时的速率v=
| 17 |
(2)若撤去电场,在盒中加一方向垂直于纸面的匀强磁场,使粒子仍恰好从e孔射出,所加磁场方向应垂直纸面向外,磁感应强度的大小B=
| E |
| 5v0 |
点评:本题分别考查了带电粒子在电场场中类平抛运动的问题和在磁场中的匀速圆周运动的问题,要求同学们能正确分析粒子的受力情况及粒子的运动情况,熟练掌握圆周运动及类平抛运动的基本公式,难度适中.

练习册系列答案
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 如图所示,abcd是一个正方形盒子.cd边的中点有一个小孔e.盒子中有沿ad方向的匀强电场.一个质量为m带电量为q的粒子从a处的小孔沿ab方向以初速度v0射入盒内,并恰好从e处的小孔射出.(忽略粒子重力)求:
如图所示,abcd是一个正方形盒子.cd边的中点有一个小孔e.盒子中有沿ad方向的匀强电场.一个质量为m带电量为q的粒子从a处的小孔沿ab方向以初速度v0射入盒内,并恰好从e处的小孔射出.(忽略粒子重力)求: 如图所示,ABCD是放在E=1.0×103V/m的水平匀强电场中的绝缘光滑竖直轨道,BCD是直径为20cm的半圆环,AB=15cm,一质量为10g,带电量1.0×10-4C的小球由静止在电场力作用下自A点沿轨道运动,求:
如图所示,ABCD是放在E=1.0×103V/m的水平匀强电场中的绝缘光滑竖直轨道,BCD是直径为20cm的半圆环,AB=15cm,一质量为10g,带电量1.0×10-4C的小球由静止在电场力作用下自A点沿轨道运动,求: (2008?潮州二模)如图所示,abcd是由导体做成的框架,其平面与水平面成θ角,质量为m的导体棒PQ与光滑导轨ab、cd接触良好,回路面积为S.整个装置放在垂直于框架平面的磁场中,磁感应强度随时间变化情况如图所示,PQ始终静止.则下面说法错误的是( )
(2008?潮州二模)如图所示,abcd是由导体做成的框架,其平面与水平面成θ角,质量为m的导体棒PQ与光滑导轨ab、cd接触良好,回路面积为S.整个装置放在垂直于框架平面的磁场中,磁感应强度随时间变化情况如图所示,PQ始终静止.则下面说法错误的是( ) 如图所示,ABCD是一个正方形盒子,CD边的中点有一个小孔O,盒子中有沿AD方向的匀强电场,场强大小为E.粒子源不断地从A处的小孔沿AB方向向盒内发射相同的带电粒子,粒子的质量为m,带电量为q,初速度为v0,在电场作用下,粒子恰好从O处的小孔射出;(带电粒子的重力和粒子间的相互作用力均可忽略) 求:
如图所示,ABCD是一个正方形盒子,CD边的中点有一个小孔O,盒子中有沿AD方向的匀强电场,场强大小为E.粒子源不断地从A处的小孔沿AB方向向盒内发射相同的带电粒子,粒子的质量为m,带电量为q,初速度为v0,在电场作用下,粒子恰好从O处的小孔射出;(带电粒子的重力和粒子间的相互作用力均可忽略) 求: 如图所示,ABCD是LED闪光灯的圆柱形封装玻璃体.玻璃体的直径为l、厚度为d,且l=2d.LED灯(可视为点光源)固定在玻璃体CD面的圆心P点,其发出的光进入玻璃体后从AB面射出.玻璃体的折射率为
如图所示,ABCD是LED闪光灯的圆柱形封装玻璃体.玻璃体的直径为l、厚度为d,且l=2d.LED灯(可视为点光源)固定在玻璃体CD面的圆心P点,其发出的光进入玻璃体后从AB面射出.玻璃体的折射率为