题目内容
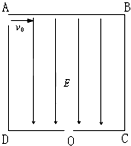 如图所示,ABCD是一个正方形盒子,CD边的中点有一个小孔O,盒子中有沿AD方向的匀强电场,场强大小为E.粒子源不断地从A处的小孔沿AB方向向盒内发射相同的带电粒子,粒子的质量为m,带电量为q,初速度为v0,在电场作用下,粒子恰好从O处的小孔射出;(带电粒子的重力和粒子间的相互作用力均可忽略) 求:
如图所示,ABCD是一个正方形盒子,CD边的中点有一个小孔O,盒子中有沿AD方向的匀强电场,场强大小为E.粒子源不断地从A处的小孔沿AB方向向盒内发射相同的带电粒子,粒子的质量为m,带电量为q,初速度为v0,在电场作用下,粒子恰好从O处的小孔射出;(带电粒子的重力和粒子间的相互作用力均可忽略) 求:①正方形盒子的边长L=?(用m,v0,q,E表示)
②该带电粒子从O孔射出时的速率v=?(用 v0表示)
分析:(1)将运动沿着水平和竖直方向正交分解,粒子在AB方向上作匀速运动,粒子在AD方向上做初速度为0的匀加速运动;
(2)运用牛顿运动定律、运动学公式和动能定理列式求解;
(2)运用牛顿运动定律、运动学公式和动能定理列式求解;
解答:解:(1)设正方形的边长为l,则有:
粒子在AB方向上作匀速运动,有:
L=v0t
粒子在AD方向上做初速度为0的匀加速运动,有:L=
at2
根据牛顿第二定律有:a=
由以上各式解得:l=
;
(2)根据动能定理,有:
qE×L=
mv2-
所以有:v=
v0;
解:①正方形盒子的边长L=
;
②该带电粒子从O孔射出时的速率v=
v0.
粒子在AB方向上作匀速运动,有:
| 1 |
| 2 |
粒子在AD方向上做初速度为0的匀加速运动,有:L=
| 1 |
| 2 |
根据牛顿第二定律有:a=
| qE |
| m |
由以上各式解得:l=
8
| ||
| qE |
(2)根据动能定理,有:
qE×L=
| 1 |
| 2 |
| 1 |
| 2 |
| m v | 2 0 |
所以有:v=
| 17 |
解:①正方形盒子的边长L=
8
| ||
| qE |
②该带电粒子从O孔射出时的速率v=
| 17 |
点评:本题关键将带电粒子的运动沿初速度方向和电场方向进行正交分解,然后根据牛顿第二定律和运动学公式列式求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,abcd是一个正方形盒子.cd边的中点有一个小孔e.盒子中有沿ad方向的匀强电场.一个质量为m带电量为q的粒子从a处的小孔沿ab方向以初速度v0射入盒内,并恰好从e处的小孔射出.(忽略粒子重力)求:
如图所示,abcd是一个正方形盒子.cd边的中点有一个小孔e.盒子中有沿ad方向的匀强电场.一个质量为m带电量为q的粒子从a处的小孔沿ab方向以初速度v0射入盒内,并恰好从e处的小孔射出.(忽略粒子重力)求: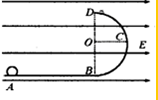 如图所示,ABCD是放在E=1.0×103V/m的水平匀强电场中的绝缘光滑竖直轨道,BCD是直径为20cm的半圆环,AB=15cm,一质量为10g,带电量1.0×10-4C的小球由静止在电场力作用下自A点沿轨道运动,求:
如图所示,ABCD是放在E=1.0×103V/m的水平匀强电场中的绝缘光滑竖直轨道,BCD是直径为20cm的半圆环,AB=15cm,一质量为10g,带电量1.0×10-4C的小球由静止在电场力作用下自A点沿轨道运动,求: (2008?潮州二模)如图所示,abcd是由导体做成的框架,其平面与水平面成θ角,质量为m的导体棒PQ与光滑导轨ab、cd接触良好,回路面积为S.整个装置放在垂直于框架平面的磁场中,磁感应强度随时间变化情况如图所示,PQ始终静止.则下面说法错误的是( )
(2008?潮州二模)如图所示,abcd是由导体做成的框架,其平面与水平面成θ角,质量为m的导体棒PQ与光滑导轨ab、cd接触良好,回路面积为S.整个装置放在垂直于框架平面的磁场中,磁感应强度随时间变化情况如图所示,PQ始终静止.则下面说法错误的是( )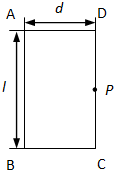 如图所示,ABCD是LED闪光灯的圆柱形封装玻璃体.玻璃体的直径为l、厚度为d,且l=2d.LED灯(可视为点光源)固定在玻璃体CD面的圆心P点,其发出的光进入玻璃体后从AB面射出.玻璃体的折射率为
如图所示,ABCD是LED闪光灯的圆柱形封装玻璃体.玻璃体的直径为l、厚度为d,且l=2d.LED灯(可视为点光源)固定在玻璃体CD面的圆心P点,其发出的光进入玻璃体后从AB面射出.玻璃体的折射率为