Question

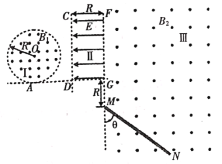
【题目】如图所示，在y轴的右侧存在磁感应强度为B、方向垂直纸面向外的匀强磁场，在x轴的上方有一平行板式加速电场．有一薄绝缘板放置在y轴处，且与纸面垂直．现在一质量为m、电荷量为q的粒子由静止经过加速电压为U的电场加速，然后以垂直于板的方向沿直线从A处穿过绝缘板，而后从x轴上的D处以与x轴负向夹角为30°的方向进入第四象限，此时再加一匀强电场，使粒子能沿直线从D点到达y轴上的C点．已知OD长为l，不计粒子的重力．求：

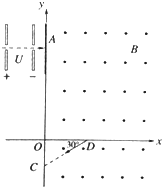
（1）粒子射入绝缘板之间的速度；

（2）粒子经过绝缘板时损失了多少动能；

（3）所加匀强电场的电场强度的大小及方向；

（4）带电粒子在y轴的右侧运行的总时间．

Answer 1

【答案】（1）qU-（3），方向与x轴正向斜向下成60°角（4）

【解析】

（1）粒子在电场中加速，由动能定理得：qU=mv2-0，

解得：v=．

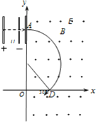
（2）粒子在磁场中做圆周运动轨迹如图所示：

由几何关系可得轨道半径：r=2l．

由牛顿第二定律得：qv′B=m，

解得：v′=．

根据能量守恒得，损失的动能为：△EK=mv2-mv′2，

解得：△EK=qU-．

（3）粒子若作直线运动，洛伦兹力与电场力相等，即：qv′B=qE，

解得：E=，方向与x轴正向斜向下成60°角．

（4）粒子在第一象限作匀速圆周运动的时间为：t1=，

粒子在第四象限做匀速直线运动的时间为：t2==，

粒子x轴右侧运行的总时间为：t=t1+t2=．