题目内容
如图所示,一根长为L=1.5m的绝缘细直杆MN,竖直固定在场强为E=1.0×105N/C、与水平方向成θ=37°角的倾斜向上的匀强电场中.杆的下端M固定一个带电小球A,电荷量Q= +4.5×10-6C;另一带电小来自球B穿在杆上可自由滑动,电荷量q= +1.0×10-6C,质量m=1.0×10-2kg,与杆之间的动摩擦因数μ=0.1.现将小球B从杆的上端N静止释放,小球B开始运动.(静电力常量k=9.0×109N·m2/C2.取g=10m/s2,sin37°=0.6,cos37°=0.8)

(1)小球B开始运动时的加速度为多大?
(2)小球B的速度最大时,距M端的高度h为多大?
(3)若小球B在下落过程的最大速度为0.77m/s,则从开始下落到速度达到最大的过程中,小球B的电势能改变了多少?
(1)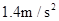 (2)1.125m(3)
(2)1.125m(3)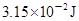
解析试题分析:(1)开始运动时小球B受重力、库仑力、杆的弹力、电场力和摩擦力,沿杆方向运动,由牛顿第二定律得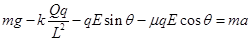
解得:
代入数据解得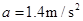
(2)小球B速度最大时合力为零,即
解得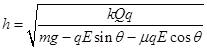
代入数据解得
h=1.125m
(3)小球B从开始运动到速度为v的过程中,设重力做功为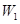 ,电场力做功为
,电场力做功为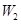 ,库仑力做功为
,库仑力做功为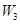 ,摩擦力做功
,摩擦力做功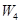 ,根据动能定理有:(或者把匀强电场和A电荷对B的作用力统称为电场力,得到正确答案照常给分)
,根据动能定理有:(或者把匀强电场和A电荷对B的作用力统称为电场力,得到正确答案照常给分)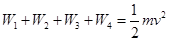
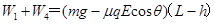
设小球的电势能改变了ΔEP,则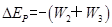
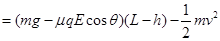
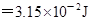
考点:电场力做功与电势能的关系
点评:对小球B进行受力分析,运用牛顿第二定律求出开始运动时的加速度大小.根据受力情况分析小球B的运动情况,找出小球B速度最大时的位置特点.由于A对B的库仑力做功是变力功,所以运用动能定理求解电场力做功.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
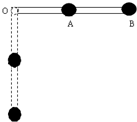 如图所示,一根长为L,质量不计的硬杆,在中点及右端各固定一个质量为m的小球,杆可带动小球在竖直平面内绕O点转动.若开始时杆处于水平位置,由静止开始释放,当杆下落到竖直位置时,下列说法中正确的是( )
如图所示,一根长为L,质量不计的硬杆,在中点及右端各固定一个质量为m的小球,杆可带动小球在竖直平面内绕O点转动.若开始时杆处于水平位置,由静止开始释放,当杆下落到竖直位置时,下列说法中正确的是( )A、B球的速率为
| ||||
B、B球的机械能减少了
| ||||
C、A球的机械能减少了
| ||||
| D、每个小球的机械能都不变 |
 如图所示,一根长为L的细杆的一端固定一质量为m的小球,整个系统绕杆的另一端在竖直面内做圆周运动,且小球恰能过最高点.已知重力加速度为g,细杆的质量不计.下列说法正确的是( )
如图所示,一根长为L的细杆的一端固定一质量为m的小球,整个系统绕杆的另一端在竖直面内做圆周运动,且小球恰能过最高点.已知重力加速度为g,细杆的质量不计.下列说法正确的是( )A、小球过最低点时的速度大小为
| ||
B、小球过最高点时的速度大小为
| ||
| C、小球过最低点时受到杆的拉力大小为5mg | ||
| D、小球过最高点时受到杆的支持力为零 |
 如图所示,一根长为L、质量为100kg的木头,其重心O在离粗端
如图所示,一根长为L、质量为100kg的木头,其重心O在离粗端 如图所示,一根长为L的轻质细线,一端固定于O点,另一端拴有一质量为m的小球,可在竖直的平面内绕O点摆动,现拉紧细线使小球位于与O点在同一竖直面内的A位置,细线与水平方向成30°角,从静止释放该小球,当小球运动至悬点正下方C位置时的速度是( )
如图所示,一根长为L的轻质细线,一端固定于O点,另一端拴有一质量为m的小球,可在竖直的平面内绕O点摆动,现拉紧细线使小球位于与O点在同一竖直面内的A位置,细线与水平方向成30°角,从静止释放该小球,当小球运动至悬点正下方C位置时的速度是( ) 如图所示,一根长为l的轻杆的一端与一个质量为m为小球相连,并可绕过另一端O点的水平轴在竖直面内自由转动,图中的a、b分别表示小球运动轨迹的最低点和最高点,已知杆能提供的最大支持力为
如图所示,一根长为l的轻杆的一端与一个质量为m为小球相连,并可绕过另一端O点的水平轴在竖直面内自由转动,图中的a、b分别表示小球运动轨迹的最低点和最高点,已知杆能提供的最大支持力为