题目内容
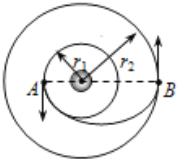
【题目】(1) 要发射一颗人造地球卫星，使它在半径为r2的预定轨道2上绕地球做匀速圆周运动，为此先将卫星发射到半径为r1的近地暂行圆轨道上绕地球做匀速圆周运动．如图所示，在A点，使卫星速度增加，从而使卫星进入一个椭圆的转移轨道1上，当卫星到达转移轨道的远地点B时，再次改变卫星速度，使它进入预定轨道2运行，试求卫星从A点到B点所需的时间．已知地球表面的重力加速度大小为g，地球的半径为R．
(2)物体在万有引力场中具有的势能叫做引力势能。若取两物体相距无穷远时的引力
势能为零，一个质量为m0的质点距质量为M0的引力源中心为r0时，其万有引力势
能
（式中G为引力常数）。若卫星在椭圆轨道1上运动的过程中，动能
和引力势能相互转化，它们的总量保持不变。已知卫星在轨道1上运动时的质量为m，
B点距地球表面的高度分别为h1、h2，经过A点的速度大小为v，地球表面的重力加速
度大小为g，地球的半径为R．请根据能量守恒定律求它经过B点时的速度大小；
（3）在（2）问的基础上，若要让这颗人造地球卫星能够挣脱太阳引力的束缚，飞到太阳系外，则必须使它的速度大于或等于第三宇宙速度。若把地球绕太阳公转的轨道近似认为是圆，且不计其它星体对飞行物体的作用力，地球的公转速度为29.8km/s，求第三宇宙速度。
【答案】（1）
（2）
（3）16.7 km/s
【解析】(1)卫星在轨道r1时，万有引力提供圆周运动向心力: 
因为物体m'在地球表面有重力等于万有引力： 
可得： 
联立解得
当卫星在椭圆轨道运行：其半长轴为： 
依开普勒第三定律： 
得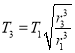
解得： 
故卫星从A到B的时间
(2)卫星在轨道上运动的过程中，由机械能守恒定律有： 
解得：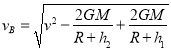 
(3)由
，可得
若摆脱地球的约束，则有： 
可得： 
同理：在地球绕太阳公转轨道运行的物体绕太阳做圆周运动时， 
摆脱太阳的约束速度为
由于随地球绕太阳公转的物体已具有地球的公转速度29.8km/s，则只需沿太阳公转方向的速度达到
即可
又因为发射地球表面的物体还需要摆脱地球约束的动能
则：发射地球表面的物体摆脱太阳约束的第三速度为v3
有： 
解得： 
