Question

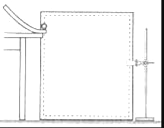
【题目】如图所示，质量均为m的三个光滑小球A、B、C用两条长均为L的细线相连，置于高为h的光滑水平桌面上（L＞h），A球刚跨过桌边，若A球、B球相继下落着地后均不再反弹，则C球离开桌面时速度的大小为多少？（不计B、C球经桌边的动能损失）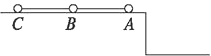

Answer 1

【答案】解：对A、B、C组成的系统，从A开始下落到它落地前瞬间过程，有机械能守恒定律得：mgh=3× mv12；对B、C组成的系统，从A落地后瞬间到B落地前瞬间，由机械能守恒定律得：
mgh=2× mv22﹣2× mv12 由上述两个方程得：
v2=
答：C球离开桌面时速度大小为
【解析】先对ABC三个物体分析，由机械能守恒可求得A落地时的速度；再对BC分析，由机械能守恒可得出C球离开桌面时的速度．
【考点精析】关于本题考查的机械能守恒及其条件，需要了解在只有重力（和弹簧弹力）做功的情形下，物体动能和重力势能（及弹性势能）发生相互转化，但机械能的总量保持不变才能得出正确答案．