��Ŀ����
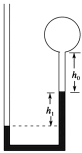
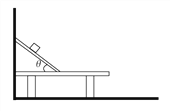
����Ŀ����ͼ��ʾ����һ�鳤L1=1.0 m��ľ����ǽ����������б�棬���Ӹ�H=0.8 m����L2=1.5 m��б����ˮƽ����ļн�������0��60������ں�̶���������m=0.2 kg��С����б�涥�˾�ֹ�ͷţ������б���Ķ�Ħ��������1=0.05������������Ķ�Ħ������Ϊ��2�����������б�������潻�Ӵ���������ʧ��(�������ٶ�ȡg=10 m/s2�����Ħ�������ڻ���Ħ����)
��1��������������ʱ������ܴ�б�濪ʼ�»���(������ֵ��ʾ)
��2������������37��ʱ�����ǡ��ͣ�������Ե��������������Ķ�Ħ��������2��(��֪sin37��=0.6��cos37��=0.8)
��3�������������ǣ�������=53��ʱ�����ص���ǽ��ľ���������������xm��
���𰸡���1��tan�ȡ�0.05��
��2����2Ϊ0.8��
��3��������xΪ1.9m��
���������⣺��1��ΪʹС����»������У�
mgsin�ȡݦ�1mgcos����
����Ӧ���������Ϊ��
tan�ȡ�0.05��
��2���˷�Ħ��������Wf=��1mgL1cos��+��2mg��L2��L1cos����
�ɶ��ܶ����ã�mgL1sin�ȩ�Wf=0
�������ݽ�ã�
��2=0.8��
��3���ɶ��ܶ����ã�
mgL1sin�ȩ�Wf=![]() mv2
mv2
��ã�v=1m/s��
����ƽ���˶�����ֱ�����У�
H=![]() gt2��
gt2��
��ã�t=0.4s��
ˮƽ����x1=vt
��ã�x1=0.4m��
���xm=x1+L2=0.4+1.5=1.9m��
�𣺣�1����������tan�ȡ�0.05��������ܴ�б�濪ʼ�»���������ֵ��ʾ��
��2������������37��ʱ�����ǡ��ͣ�������Ե������������Ķ�Ħ��������2Ϊ0.8��
��3�������������ǣ�������=53��ʱ�����ص���ǽ��ľ������������xΪ1.9m��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�