题目内容
18.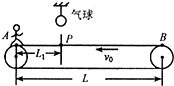 趣味运动会上有一个项目是在传送带上完成的.如图,A为传送带的左端点,B为右端点,P的正上方天花板上悬挂一个气球,AB间传送带的长度L=31m,P与A的距离L1=9m,传送带以v0=1m/s的恒定速率向左运动.比赛中,挑战者(视为质点)在A点相对地面静止,听到哨声后开始以a1=2m/s2的加速度向右匀加速运动到P,在刺破气球时不慎跌倒,经△t=2s爬起,然后又以a2=1m/s2的加速度,在传送带上匀加速到B点.假设从摔倒至爬起的过程中挑战者与传送带始终相对静止,不计刺破气球的时间.求:
趣味运动会上有一个项目是在传送带上完成的.如图,A为传送带的左端点,B为右端点,P的正上方天花板上悬挂一个气球,AB间传送带的长度L=31m,P与A的距离L1=9m,传送带以v0=1m/s的恒定速率向左运动.比赛中,挑战者(视为质点)在A点相对地面静止,听到哨声后开始以a1=2m/s2的加速度向右匀加速运动到P,在刺破气球时不慎跌倒,经△t=2s爬起,然后又以a2=1m/s2的加速度,在传送带上匀加速到B点.假设从摔倒至爬起的过程中挑战者与传送带始终相对静止,不计刺破气球的时间.求:(1)挑战者从A运动至气球处所用时间t1是多少;
(2)从摔倒到爬起随传送带运动的位移X1是多少;
(3)挑战者从A到达B所需的时间.
分析 (1)根据匀变速直线运动的位移时间公式求出挑战者从A运动到气球处所用的时间;
(2)根据匀速直线运动的位移公式求出挑战者从摔倒到爬起随传送带运动的位移;
(3)根据位移时间公式求出P到B的时间,结合A到P的时间,以及摔倒到爬起的时间,得出挑战者从A到达B的时间.
解答 解:(1)取地面为参考系,挑战者从A运动至气球处所用时间为t1,则:
L1=$\frac{1}{2}{a}_{1}{{t}_{1}}^{2}$ 得,
则挑战者从A运动到气球处的时间 t1=$\sqrt{\frac{2{L}_{1}}{{a}_{1}}}=\sqrt{\frac{2×9}{2}}s=3s$.
(2)从摔倒到爬起随传送带位移为x1,则:
x1=-v0•△t
代入数据解得 x1=2m
(3)运动员从爬起到B端位移为x,时间为t2,则:
x=L-L1-x1
位移x=$-{v}_{0}{t}_{2}+\frac{1}{2}{a}_{2}{{t}_{2}}^{2}$,
挑战者从左端到达右端全过程所需的时间为t,则:
t=t1+△t+t2
代入数据联立解得:t=13s
答:(1)挑战者从A运动至气球处所用时间t1是3s;
(2)从摔倒到爬起随传送带运动的位移x1是2m;
(3)挑战者从A到达B所需的时间为13s.
点评 解决本题的关键理清挑战者在整个过程中的运动规律,结合运动学公式灵活求解,难度不大.

练习册系列答案
相关题目
9. 如图是“神州”系列肮天飞船返回舱返回地面的示意图,其过程可简化为:打开降落伞一段时间后,整个装置匀速下降,为确保安全着陆.需
如图是“神州”系列肮天飞船返回舱返回地面的示意图,其过程可简化为:打开降落伞一段时间后,整个装置匀速下降,为确保安全着陆.需
点燃返问舱的缓冲火 箭,在火箭喷气过程中返回舱做减速直线运动,则( )
 如图是“神州”系列肮天飞船返回舱返回地面的示意图,其过程可简化为:打开降落伞一段时间后,整个装置匀速下降,为确保安全着陆.需
如图是“神州”系列肮天飞船返回舱返回地面的示意图,其过程可简化为:打开降落伞一段时间后,整个装置匀速下降,为确保安全着陆.需点燃返问舱的缓冲火 箭,在火箭喷气过程中返回舱做减速直线运动,则( )
| A. | 舱在喷气过程中处于失重状态 | |
| B. | 火箭开始喷气瞬间伞绳对返回舱的拉力不变 | |
| C. | 火箭开始喷气瞬间返回舱获得向上加速度 | |
| D. | 返问舱在喷气过程中(忽略质量变化)机械能在增加 |
6. 如图所示,两个半径不同,内壁光滑的半圆轨道固定在地面上.一个小球先后从与球心在同一水平高度上的A、B两点由静止开始自由滑下,通过轨道最低点( )
如图所示,两个半径不同,内壁光滑的半圆轨道固定在地面上.一个小球先后从与球心在同一水平高度上的A、B两点由静止开始自由滑下,通过轨道最低点( )
 如图所示,两个半径不同,内壁光滑的半圆轨道固定在地面上.一个小球先后从与球心在同一水平高度上的A、B两点由静止开始自由滑下,通过轨道最低点( )
如图所示,两个半径不同,内壁光滑的半圆轨道固定在地面上.一个小球先后从与球心在同一水平高度上的A、B两点由静止开始自由滑下,通过轨道最低点( )| A. | 小球对两轨道的压力相同 | B. | 小球对两轨道的压力不同 | ||
| C. | 小球的向心加速度相同 | D. | 小球的速度相同 |
13.一物体从距离地面H高处自由下落,当其重力势能等于动能的3倍时(以地面为零势能面),物体的速度为( )
| A. | $\frac{1}{2}$$\sqrt{2gH}$ | B. | $\sqrt{gH}$ | C. | $\sqrt{2gH}$ | D. | 2$\sqrt{gH}$ |
3. 质量为2kg的质点在竖直面内斜向下做曲线运动,它在竖直方向的速度图象如图甲所示,在水平方向的位移图象如图乙所示.g取10m/s2.则( )
质量为2kg的质点在竖直面内斜向下做曲线运动,它在竖直方向的速度图象如图甲所示,在水平方向的位移图象如图乙所示.g取10m/s2.则( )
 质量为2kg的质点在竖直面内斜向下做曲线运动,它在竖直方向的速度图象如图甲所示,在水平方向的位移图象如图乙所示.g取10m/s2.则( )
质量为2kg的质点在竖直面内斜向下做曲线运动,它在竖直方向的速度图象如图甲所示,在水平方向的位移图象如图乙所示.g取10m/s2.则( )| A. | 2s时刻,质点速度大小是5 m/s | |
| B. | 2s时刻,质点速度大小是4 m/s | |
| C. | 前2s内质点的重力势能减少了120 J | |
| D. | 前2s内质点的机械能减少了40 J |
 如图所示,半径为R的光滑金属环竖直放置,环上套有一质量为m的小球,小球开始时静止于最低点.现给小球一冲击,使它以初速度v0沿环上滑,已知v0=$\sqrt{6Rg}$.求:
如图所示,半径为R的光滑金属环竖直放置,环上套有一质量为m的小球,小球开始时静止于最低点.现给小球一冲击,使它以初速度v0沿环上滑,已知v0=$\sqrt{6Rg}$.求: 在一个竖直面内固定一个半径为R的光滑半圆环,AB为直径,小球从A处沿圆环内侧切线方向射入并在环内运动,如图所示,若小球刚好落在圆心O点,求在A点入射时的初速度v0多大?(已知R=$\sqrt{3}$m,g=10m/s2)
在一个竖直面内固定一个半径为R的光滑半圆环,AB为直径,小球从A处沿圆环内侧切线方向射入并在环内运动,如图所示,若小球刚好落在圆心O点,求在A点入射时的初速度v0多大?(已知R=$\sqrt{3}$m,g=10m/s2)