题目内容
6. 如图所示,两个半径不同,内壁光滑的半圆轨道固定在地面上.一个小球先后从与球心在同一水平高度上的A、B两点由静止开始自由滑下,通过轨道最低点( )
如图所示,两个半径不同,内壁光滑的半圆轨道固定在地面上.一个小球先后从与球心在同一水平高度上的A、B两点由静止开始自由滑下,通过轨道最低点( )| A. | 小球对两轨道的压力相同 | B. | 小球对两轨道的压力不同 | ||
| C. | 小球的向心加速度相同 | D. | 小球的速度相同 |
分析 小球从与球心在同一水平高度的A、B两点由静止开始自由下滑过程中,受到重力和支持力作用,只有重力做功,机械能守恒,由机械能守恒定律可求出小球到最低点的速度,然后由向心加速度公式求向心加速度,由牛顿第二定律求出支持力,进而来比较向心加速度大小和压力大小.
解答 解:D、根据动能定理mgR=$\frac{1}{2}$mv2,
v=$\sqrt{2gL}$ 所以A球的速度大于B球的速度,故D错误.
A、B、在最低点,根据牛顿第二定律得:
F-mg=m$\frac{{v}^{2}}{R}$,
得F=mg+m$\frac{{v}^{2}}{R}$=3mg,与半径的大小无关.故A正确,B错误.
C、在最低点的向心加速度:$a=\frac{{v}^{2}}{R}=\frac{2gR}{R}=2g$,两球小球的向心加速度相同.故C正确.
故选:AC
点评 小球下滑过程中,机械能守恒,由机械能守恒定律、牛顿第二定律、向心力公式分别求出小球在最低点的压力和向心加速度,可以看出它们与圆轨道的半径无关,这个结论要理解记住.

练习册系列答案
相关题目
16.如图所示,线圈L的电阻不计,则( )
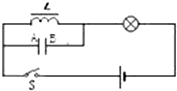

| A. | S刚闭合时,灯立即正常发光 | |
| B. | 当灯正常发光时,电容器不带电 | |
| C. | S断开瞬间,灯熄灭,电容器不带电 | |
| D. | S断开瞬间,灯熄灭,电容器的A板带负电 |
17.试验中对提高测量结果精度有利的建议是( )
| A. | 单摆的摆线不能太短 | |
| B. | 单摆的摆球密度尽可能大 | |
| C. | 单摆的摆角越大越好 | |
| D. | 从平衡位置开始计时,测量一次全振动的时间作为单摆周期 |
1.下列实例中,机械能守恒的是( )
| A. | 物体沿光滑曲面滑下 | B. | 拉着一个物体沿光滑斜面匀速上升 | ||
| C. | 降落伞吊着重物在空气中匀速下落 | D. | 氢气球匀速上升 |
11.下列物体中,机械能一定守恒的是( )
| A. | 受到平衡力作用而运动的物体 | B. | 只受重力作用而运动的物体 | ||
| C. | 只受重力和拉力作用而运动的物体 | D. | 在水平面上做圆周运动的汽车 |
15. 如图所示的电路中,L是自感系数很大的、用铜导线绕成的线圈,其电阻可以忽略不计,开关S原来是闭合的,当开关S断开瞬间,则( )
如图所示的电路中,L是自感系数很大的、用铜导线绕成的线圈,其电阻可以忽略不计,开关S原来是闭合的,当开关S断开瞬间,则( )
①L中的电流方向不变
②灯泡D要过一会儿才熄灭
③LC电路将产生电磁振荡,刚断开瞬间,磁场能最大
④电容器将放电,电场能将变为磁场能.
 如图所示的电路中,L是自感系数很大的、用铜导线绕成的线圈,其电阻可以忽略不计,开关S原来是闭合的,当开关S断开瞬间,则( )
如图所示的电路中,L是自感系数很大的、用铜导线绕成的线圈,其电阻可以忽略不计,开关S原来是闭合的,当开关S断开瞬间,则( )①L中的电流方向不变
②灯泡D要过一会儿才熄灭
③LC电路将产生电磁振荡,刚断开瞬间,磁场能最大
④电容器将放电,电场能将变为磁场能.
| A. | ①④ | B. | ②③ | C. | ①③ | D. | ①②③ |
16.关于电动势下列说法正确的是( )
| A. | 电源电动势等于电源正负极之间的电势差 | |
| B. | 用电压表直接测量电源两极得到的电压数值,实际上总略小于电源电动势的准确值 | |
| C. | 电源电动势总等于内、外电路上的电压之和,所以它的数值与外电路的组成有关 | |
| D. | 电源是电能转化为其他形式能量的装置 |
 小鑫在超市看到,电梯上有人时运动得快,没人时运动得慢.如图是小鑫上网搜索到的这种电梯的部分控制电路(R是一个压敏电阻),并进行了如下分析:通电后电磁铁的上端是S极,当有人走上电梯后,通过电动机的电流变大(选填“变大”或“变小”),电动机转速变快,使电梯运动变快.
小鑫在超市看到,电梯上有人时运动得快,没人时运动得慢.如图是小鑫上网搜索到的这种电梯的部分控制电路(R是一个压敏电阻),并进行了如下分析:通电后电磁铁的上端是S极,当有人走上电梯后,通过电动机的电流变大(选填“变大”或“变小”),电动机转速变快,使电梯运动变快.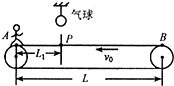 趣味运动会上有一个项目是在传送带上完成的.如图,A为传送带的左端点,B为右端点,P的正上方天花板上悬挂一个气球,AB间传送带的长度L=31m,P与A的距离L1=9m,传送带以v0=1m/s的恒定速率向左运动.比赛中,挑战者(视为质点)在A点相对地面静止,听到哨声后开始以a1=2m/s2的加速度向右匀加速运动到P,在刺破气球时不慎跌倒,经△t=2s爬起,然后又以a2=1m/s2的加速度,在传送带上匀加速到B点.假设从摔倒至爬起的过程中挑战者与传送带始终相对静止,不计刺破气球的时间.求:
趣味运动会上有一个项目是在传送带上完成的.如图,A为传送带的左端点,B为右端点,P的正上方天花板上悬挂一个气球,AB间传送带的长度L=31m,P与A的距离L1=9m,传送带以v0=1m/s的恒定速率向左运动.比赛中,挑战者(视为质点)在A点相对地面静止,听到哨声后开始以a1=2m/s2的加速度向右匀加速运动到P,在刺破气球时不慎跌倒,经△t=2s爬起,然后又以a2=1m/s2的加速度,在传送带上匀加速到B点.假设从摔倒至爬起的过程中挑战者与传送带始终相对静止,不计刺破气球的时间.求: