Question

【题目】如图所示，AB为倾角θ＝37°的斜面轨道，轨道AC部分光滑，CB部分粗糙，一质量m＝2kg的小物块与斜面BC间的动摩擦因数μ＝0.25；BP为圆心角等于143°，半径R＝0.5m的竖直光滑圆弧形轨道，两轨道相切于B点，P、O两点在同一竖直线上；轻弹簧一端固定在A点，另一端在斜面上C点处，已知sin37°＝0.6，cos37°＝0.8，g取10m/s2。

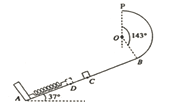
(1)若小物块静止在弹簧上端，求弹簧的弹力大小F；

(2)若小物块在B点以初速度v0＝3m/s沿斜面向下运动，至D点时速度为0．已知斜面BC部分长度sBC＝1m，CD部分长度sCD＝0.2m。

① 求弹簧被压缩到D点时的弹性势能Ep；

② 若改变小物块在B点向下的初速度vB，使小物块在沿轨道运动的过程中不脱离轨道，求vB的范围。

Answer 1

【答案】(1)12N；(2)①19.4J；②vB≤4m/s

【解析】

根据“斜面轨道…竖直光滑圆弧形轨道”、“弹簧被压缩到D点时的弹性势能”、“不脱离轨道”可知，本题考察物块在斜面和圆弧轨道运动相结合的问题。根据机械能规律解决运动类问题的方法，运用平衡条件、动能定理、临界条件、功能关系等知识列式求解。

(1)物块静止在弹簧上端时，受到重力、弹簧的弹力及斜面的支持力，由平衡条件得：

(2) ① 物块从B到D的过程，重力、弹簧以及摩擦力做功，由能量守恒定律得:

代入数据解得：

② 要使小物块在沿轨道运动的过程中不脱离轨道，临界情况是小球反弹后上升到与圆心O等高处

设物块由弹簧反弹恰能上升到与O等高的点时对应的初速度为v，对物块从下降到反弹上升到与O等高处的过程，由能量守恒定律得：

解得

所以使小物块在沿轨道运动的过程中不脱离轨道，vB的范围为