题目内容

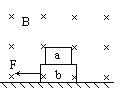
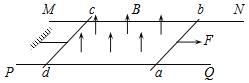
【题目】如图所示，水平地面上有两个静止的小物块a和b，其连线与墙垂直；a和b相距l，b与墙之间也相距l；a的质量为m，b的质量为m。两物块与地面间的动摩擦因数均相同。现使a以初速度v0向右滑动。此后a与b发生弹性碰撞，但b没有与墙发生碰撞。重力加速度大小为g。 求物块与地面间的动摩擦因数满足的条件。

【答案】 ≤ μ <

【解析】

设物块与地面间的动摩擦因数为μ；若要物块a、b能够发生碰撞，应有

mv02>μmgl ①

即

μ< ②

设在a、b发生弹性碰撞前的瞬间，a的速度大小为v1.由能量守恒定律得

③

设在a、b碰撞后的瞬间，a、b的速度大小分别为v1′、v2′，以向右为正方向，由动量守恒和能量守恒有

mv1＝mv1′＋mv2′ ④

⑤

联立④⑤式解得

v2′＝v1 ⑥

由题意，b没有与墙发生碰撞，由功能关系可知

⑦

联立③⑥⑦式，可得

⑧

联立②⑧式得，a与b发生弹性碰撞，但b没有与墙发生碰撞的条件为 ≤ μ <

练习册系列答案
相关题目

【题目】某同学用伏安法测一节干电池的电动势和内阻，现备有下列器材：

A．被测干电池一节

B．电流表：量程0～0.6A，内阻0.1Ω

C．电流表：量程0～3A，内阻0.024Ω

D．电压表：量程0～3V，内阻未知

E．电压表：量程0～15V，内阻未知

F．滑动变阻器：0～10Ω，2A

G．滑动变阻器：0～100Ω，1A

H．开关、导线若干

伏安法测电池电动势和内阻的实验中，由于电流表和电压表内阻的影响，测量结果存在系统误差．在现有器材的条件下，要尽可能准确地测量电池的电动势和内阻．

(1)在上述器材中请选择适当的器材：________(填写选项前的字母)；

(2)在图甲方框中画出相应的实验电路图_______；

(3)根据实验中电流表和电压表的示数得到了如图乙所示的U－I图象，则在修正了实验系统误差后，干电池的电动势E＝________V，内电阻r＝________Ω.

【题目】如图所示，a为带正电的小物块，b是一不带电的绝缘物块，a、b叠放于粗糙的水平地面上，地面上方有垂直纸面向里的匀强磁场，现用水平恒力F拉b物块，使a、b一起无相对滑动地向左加速运动，在加速运动阶段：( )

A. a、b一起运动的加速度减小

B. a、b一起运动的加速度增大

C. a、b物块间的摩擦力减小

D. a、b物块间的摩擦力增大

【题目】如图所示，坐标系xOy在竖直平面内，y轴的正方向竖直向上，y轴的右侧广大空间存在水平向左的匀强电场E1=2N/C，y轴的左侧广大空间存在匀强磁场和电场，磁场方向垂直纸面向外，B=1T，电场方向竖直向上，E2=2N/C。t=0时刻，一个带正电的质点在O点以的初速度沿着与x轴负方向成45°角射入y轴的左侧空间，质点的电量为 ，质量为 ，重力加速度g取10m/s2．求：

(1)质点从O点射入后第一次通过y轴的位置；

(2)质点从O点射入到第二次通过y轴所需时间；

(3)E1为何值时，质点从O点射入恰好第二次通过y轴时经过O点。

【题目】如图所示，用细圆管组成的光滑轨道AB部分平直，BC部分是处于竖直平面内半径为R的半圆，圆管截面半径rR。有一质量为m，半径比r略小的光滑小球以水平初速度v0射入圆管。

(1)若要小球能从C端出来，初速度v0最小需多大？

(2)在小球从C端出来的瞬间，管壁对小球的压力大小为，那么小球的初速度应为多少？

【题目】手机、电脑等电器已经普及到人们的日常生活中，这些电器都要用到锂电池。某同学利用下列器材测定一节锂电池的电动势和内阻，锂电池的电动势约为3V。

A．量程是0.6A，内阻约为0.5Ω的电流表

B．量程是3V，内阻是6kΩ的电压表

C．量程是15V，内阻是30kΩ的电压表

D．阻值为0～1kΩ，额定电流为0.5A的滑动变阻器

E．阻值为0～10Ω，额定电流为2A的滑动变阻器

F．定值电阻4Ω，额定功率4W

G．开关S一个，导线若干

（1）这位同学设计的电路图中的导线应连接到__________处；（填“①”或“②”）

（2）为了减小实验误差，电压表应选择__________；（填器材前的序号）

（3）为了使电压表和电流表的读数变化比较明显，滑动变阻器应选择__________；（填器材前的序号）

（4）用上图中的实验电路进行测量，读出电压表和电流表的读数，画出对应的U－I图线如图所示，由图线可得该锂电池的电动势E＝__________V，内阻r＝__________Ω。（计算结果都保留两位有效数字）

【题目】2018年12月8日我国成功发射了嫦娥四号探测器，它实现了人类首次月球背面着陆探测.12日16时39分，探测器在距月面129km处成功实施发动机点火，约5分钟后，探测器顺利进入距月面100km的圆形轨道，运行一段时间后择机着陆月球表面，下列说法正确的有 (　　)

A. 探测器发射速度大于7.9km/s

B. 探测器在距月面129km处发动机点火加速

C. 从点火到进入圆轨道，探测器位移是29km

D. 若已知引力常量、圆形轨道半径及探测器在其上运行周期，可估算月球质量

【题目】如图，拖着旧橡胶轮胎跑是身体耐力训练的一种有效方法。如果某受训者拖着轮胎在水平直道上跑了200m，那么下列说法正确的是（　　）

A.摩擦力对轮胎做了负功B.重力对轮胎做了正功

C.拉力对轮胎不做功D.支持力对轮胎做了正功

【题目】如图所示，在方向竖直向上的磁感应强度为B的匀强磁场中有两条光滑固定的平行金属导轨MN、PQ，导轨足够长，间距为L，其电阻不计，导轨平面与磁场垂直，ab、cd为两根垂直于导轨水平放置的金属棒，其接入回路中的电阻均为R，质量均为m，与金属导轨平行的水平轻质细线一端固定，另一端与cd棒的中点连接。一开始细线处于伸直状态，ab棒在平行于导轨的水平拉力F的作用下从静止开始以恒定加速度a向右做匀加速直线运动，经时间t0细线被拉断，两根金属棒运动时始终与导轨接触良好且与导轨相垂直。求：

（1）细线能承受的最大拉力F0；

（2）绳拉断前的过程中通过导体ab的电量q；

（3）若在细线被拉断瞬间撤去拉力F，求两根金属棒之间距离增量△x的最大值及绳断后回路中产生的总焦耳热。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网