题目内容
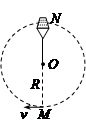
(20分)如图所示,在水平向左的匀强电场中,一带电小球质量为m,电量为-q。用绝缘轻绳(不伸缩)悬于O点,平衡时小球位于A点,此时绳与竖直方向的夹角θ=30°。绳长为l,AO=CO=DO=l,OD水平,OC竖直。求:
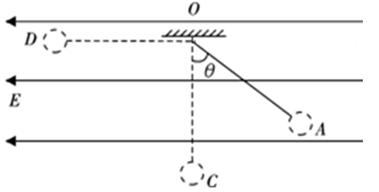
(1)电场强度E
(2)当小球移到D点后,让小球由静止自由释放,小球向右摆动过程中的最大速率和该时刻轻绳中张力(计算结果可带根号)。

(1)电场强度E
(2)当小球移到D点后,让小球由静止自由释放,小球向右摆动过程中的最大速率和该时刻轻绳中张力(计算结果可带根号)。
(1)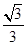
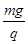 (2)F=
(2)F=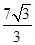 mg
mg
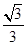
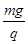 (2)F=
(2)F=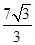 mg
mg试题分析:(1)有平衡条件得:
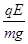 =tan30°(2分)
=tan30°(2分)E=
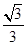
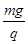 (2分)
(2分)(2) 当小球移到D点后,让小球由静止自由释放,小球先做匀加速直线运动,运动到与竖直方向成30°时绳绷直,关于OC对称,设此时速度为VB
由牛顿第二定律得;
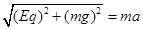 解得a=
解得a=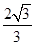 g(2分)
g(2分)对匀加速过程有V
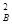 =2al(2分)
=2al(2分)绳绷直后,沿绳方向速度VBX不变,垂直绳方向速度变为0
VBX=VBcos30°(3分)
到达A点时切向加速度为0,速度达到最大值
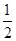 m V
m V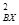 +qEl=
+qEl=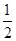 mV
mV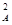 (3分)
(3分)解得V
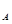 =
=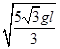 (2分)
(2分)轻绳中张力
F-
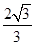 mg=
mg=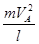 (2分)
(2分)解得F=
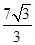 mg (2分)
mg (2分)
练习册系列答案
相关题目

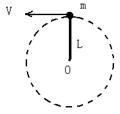
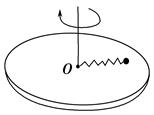


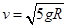 。则下列判断正确的是( )
。则下列判断正确的是( )