题目内容
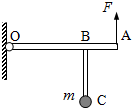
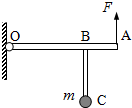 如图所示,长l的轻杆OA的左端O点为固定转动轴,杆上B点处垂直固定着一个轻杆BC,已知OB=
如图所示,长l的轻杆OA的左端O点为固定转动轴,杆上B点处垂直固定着一个轻杆BC,已知OB=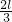 ,BC=
,BC= ,C点固定一质量为m的小球(可视为质点).现在A端施加一始终垂直于OA的力F,缓慢地将杆从图示位置提起,当OA转过θ=________角时,力F有最大值,最大值为Fm=________.
,C点固定一质量为m的小球(可视为质点).现在A端施加一始终垂直于OA的力F,缓慢地将杆从图示位置提起,当OA转过θ=________角时,力F有最大值,最大值为Fm=________.
37° 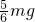
分析:以O支点,缓慢地将杆从图示位置提起的过程中,杆的力矩平衡,由力矩平衡条件得出F与θ的关系式,由数学知识求解F的最大值及θ的值.
解答:设OA转过的角度为θ.
以O支点,缓慢地将杆从图示位置提起的过程中,由力矩平衡条件得
Fl=mg(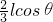 +
+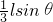 )
)
得F=mg( +
+ )=
)=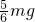 sin(α+θ),式中,tanα=
sin(α+θ),式中,tanα= =
= ,得α=53°
,得α=53°
则根据数学知识得:当θ=37°,α+θ=90°,sin(α+θ)最大,F有最大值,最大值Fm=
故答案为:37°,
点评:本题采用数学上函数法求解F的最大值,考查运用数学知识解决物理问题的能力.
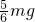
分析:以O支点,缓慢地将杆从图示位置提起的过程中,杆的力矩平衡,由力矩平衡条件得出F与θ的关系式,由数学知识求解F的最大值及θ的值.
解答:设OA转过的角度为θ.
以O支点,缓慢地将杆从图示位置提起的过程中,由力矩平衡条件得
Fl=mg(
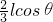 +
+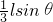 )
)得F=mg(
 +
+ )=
)=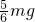 sin(α+θ),式中,tanα=
sin(α+θ),式中,tanα= =
= ,得α=53°
,得α=53°则根据数学知识得:当θ=37°,α+θ=90°,sin(α+θ)最大,F有最大值,最大值Fm=

故答案为:37°,

点评:本题采用数学上函数法求解F的最大值,考查运用数学知识解决物理问题的能力.

练习册系列答案
相关题目
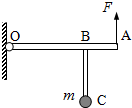 如图所示,长l的轻杆OA的左端O点为固定转动轴,杆上B点处垂直固定着一个轻杆BC,已知OB=
如图所示,长l的轻杆OA的左端O点为固定转动轴,杆上B点处垂直固定着一个轻杆BC,已知OB=
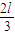 ,BC=
,BC= ,C点固定一质量为m的小球(可视为质点).现在A端施加一始终垂直于OA的力F,缓慢地将杆从图示位置提起,当OA转过θ= 角时,力F有最大值,最大值为Fm= .
,C点固定一质量为m的小球(可视为质点).现在A端施加一始终垂直于OA的力F,缓慢地将杆从图示位置提起,当OA转过θ= 角时,力F有最大值,最大值为Fm= .