题目内容
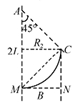
如图所示,左侧装置内存在着匀强磁场和方向竖直向下的匀强电场,装置上下两极板问电势差为U,间距为L;右侧为“台形”匀强磁场区域ACDH,其中,AH//CD, =4L。一束电荷量大小为q、质量不等的带电粒子(不计重力、可视为质点),从狭缝S1射入左侧装置中恰能沿水平直线运动并从狭缝S2射出,接着粒子垂直于AH、由AH的中点M射入“台形”区域,最后全部从边界AC射出。若两个区域的磁场方向均水平(垂直于纸面向里)、磁感应强度大小均为B,“台形”宽度
=4L。一束电荷量大小为q、质量不等的带电粒子(不计重力、可视为质点),从狭缝S1射入左侧装置中恰能沿水平直线运动并从狭缝S2射出,接着粒子垂直于AH、由AH的中点M射入“台形”区域,最后全部从边界AC射出。若两个区域的磁场方向均水平(垂直于纸面向里)、磁感应强度大小均为B,“台形”宽度 =L,忽略电场、磁场的边缘效应及粒子间的相互作用。
=L,忽略电场、磁场的边缘效应及粒子间的相互作用。

(1)判定这束粒子所带电荷的种类,并求出粒子速度的大小;
(2)求出这束粒子可能的质量最小值和最大值;
(3)求出(2)问中偏转角度最大的粒子在“台形”区域中运动的时间。
 =4L。一束电荷量大小为q、质量不等的带电粒子(不计重力、可视为质点),从狭缝S1射入左侧装置中恰能沿水平直线运动并从狭缝S2射出,接着粒子垂直于AH、由AH的中点M射入“台形”区域,最后全部从边界AC射出。若两个区域的磁场方向均水平(垂直于纸面向里)、磁感应强度大小均为B,“台形”宽度
=4L。一束电荷量大小为q、质量不等的带电粒子(不计重力、可视为质点),从狭缝S1射入左侧装置中恰能沿水平直线运动并从狭缝S2射出,接着粒子垂直于AH、由AH的中点M射入“台形”区域,最后全部从边界AC射出。若两个区域的磁场方向均水平(垂直于纸面向里)、磁感应强度大小均为B,“台形”宽度 =L,忽略电场、磁场的边缘效应及粒子间的相互作用。
=L,忽略电场、磁场的边缘效应及粒子间的相互作用。
(1)判定这束粒子所带电荷的种类,并求出粒子速度的大小;
(2)求出这束粒子可能的质量最小值和最大值;
(3)求出(2)问中偏转角度最大的粒子在“台形”区域中运动的时间。
(1)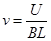 (2)
(2)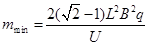 ,
,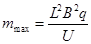 (3)
(3)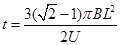
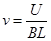 (2)
(2)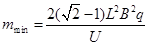 ,
,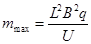 (3)
(3)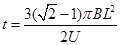
试题分析:(1)由于粒子在“台形”磁场中从边界AC射出,可知粒子带正电
由于粒子在左侧正交电磁场中沿直线通过,且洛伦兹力不做功,故粒子速率不变
故有:
 ,而
,而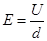 ,所以
,所以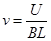
(2)在台形区域内,粒子匀速圆周运动,根据牛顿第二定律,有
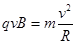
由上式知:当粒子质量最小时,R最小,粒子运动轨迹恰好与AC相切,如图,
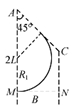
当粒子质量有最大值时,R最大,粒子运动轨迹恰好过C点,如图
根据几何关系有
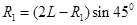 ,所以
,所以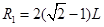
因为
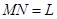 ,所以
,所以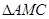 是等边三角形,
是等边三角形,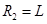
解得:
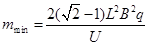 ,
,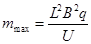
(3)粒子运动周期
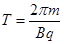
粒子沿质量最小时的轨迹运动时对应圆心角最大,有
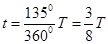
解得
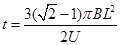

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
 ,
, .不计粒子重力,求:
.不计粒子重力,求:



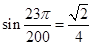 )求:
)求:
 ;
;
