Question

【题目】如图所示的塔吊臂上有一可以沿水平方向运动的小车A，小车下装有吊着物体B的吊钩，在小车A与物体B以相同的水平速度沿吊臂方向匀速运动的同时，吊钩将物体B向上吊起，A、B之间的距离以d＝H－2t2(式中H为吊臂离地面的高度)规律变化，则物体做(　 　)

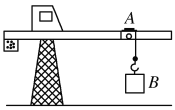
A. 速度大小不变的曲线运动

B. 速度大小增加的直线运动

C. 加速度大小、方向均变化的曲线运动

D. 加速度大小、方向均不变的曲线运动

Answer 1

【答案】D

【解析】

物体B水平方向做匀速运动，竖直方向做匀加速直线运动，根据题意d=H-2t2，结合位移时间关系公式，可以得出加速度的大小；合运动与分运动的速度、加速度都遵循平行四边形定则，由于合速度大小和方向都变化，得出物体的运动特点和合加速度的情况．

物体B参加了两个分运动，水平方向的匀速直线运动和竖直方向的匀加速直线运动；对于竖直分运动，结合位移-时间关系公式x=v0t+at2，可得到d=H-x=H-（v0yt+at2）；又根据题意d=H-2t2；对比两式可得出：竖直分运动的加速度的大小为ay=4m/s2；竖直分运动的初速度为v0y=0；故竖直分速度为vy=4t；物体的水平分速度不变；合运动的速度为竖直分速度与水平分速度的合速度，遵循平行四边形定则，故合速度的方向不断变化，物体一定做曲线运动，合速度的大小，故合速度的大小也一定不断变大，故AB错误；水平分加速度等于零，故合加速度等于竖直分运动的加速度，因而合加速度的大小和方向都不变，故C错误，D正确；故选D。