Question

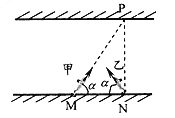
【题目】如图所示，甲、乙两船在同一条河流中同时开始渡河，M、N分别是甲、乙两船的出发点，两船头与河岸均成α角，甲船船头恰好对准N点的正对岸P点，经过一段时间乙船恰好到达P点，如果两船划船速度大小相同且不变，假设若两船相遇时，不影响各自的航行，下列判断正确的是（ ）

A. 两船渡河时间也可能不同 B. 甲船也能到达正对岸

C. 两船一定会在NP直线上相遇 D. 渡河过程中两船可能不会相遇

Answer 1

【答案】C

【解析】

由运动的独立性可知，渡河时间取决于船垂直于河岸的速度，由两船的速度可求得渡河时间；根据乙船的合运动可知船速与水速的关系；先求得甲船沿水流方向的速度，根据渡河时间可求得甲过河时在水流方向上通过的距离，则可判断在何处靠岸．

由于两船的速度大小相等，且与河岸的夹角相同，所以船速在垂直于河岸方向上的分速度相等；根据运动的独立性原理，船速度平行于河岸的分量将不影响船行驶到对岸所用的时间，所以两船同时到岸，故A错误； 设水流的速度为vs，船的速度为vc，乙船恰好到达P点说明乙的合速度的方向垂直于河岸的方向，则：vccosα=vs；甲船沿水流方向的速度为vccosα+vs=2vs，在相同的时间内，甲船通过的位移x甲=2vst，设河的宽度为d，船到达对岸的时间为：，M与N之间的距离为： ；故甲船沿水流方向通过的位移为：x甲=2vst=2×vccosα×=2L；故甲船在P点的下游靠岸，在两船靠岸以前会相遇，由几何关系可知，两船的相遇点一定在PN连线的中点处，故BD错误，C正确；故选C。