题目内容
15.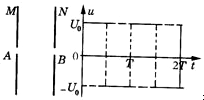 如图甲所示两平行金属板M、N相距d,两极板上有两个正对的小孔A和B,其连线与板面垂直,在两板上加有如图乙所示的交流电压u,交流电压的周期为T,在t=0时刻,N板的电势比M板高U0,一个带正电的粒子(质量为m,电荷量为q)经电压为U(U<U0)的加速电场加速后,从A孔垂直于M板射入两板间.
如图甲所示两平行金属板M、N相距d,两极板上有两个正对的小孔A和B,其连线与板面垂直,在两板上加有如图乙所示的交流电压u,交流电压的周期为T,在t=0时刻,N板的电势比M板高U0,一个带正电的粒子(质量为m,电荷量为q)经电压为U(U<U0)的加速电场加速后,从A孔垂直于M板射入两板间.(1)对于加速电压U,存在一个值Uc,当U>Uc时,带电粒子能够沿一个方向运动,一直到从B孔射出,求Uc大小;
(2)加速电压U多大时,带电粒子恰好返回A孔?(忽略重力)
分析 (1)带电粒子经加速电场加速后在MN间的电场中先做减速运动,后做加速运动,若带电粒子减速至O前加速度就反向,则带电粒子将沿一个方向继续运动,对应临界状态就是在第一个半周期内速度刚好减至O时电场反向,继续做加速运动穿过电场;
(2)带电粒子不会穿过电场时要求粒子在第一个半周期内要退出电场,根据匀变速运动规律知,粒子在第一个四分之一周期内速度要减至O,从而得出速度与电场强度的关系,再根据动能定理求加速电压U.
解答 解:(1)由于加速电压U<U0,则带正电微粒不能在第一个半周期内穿过电场,从B孔射出.微粒进入电场后,在交流电的半个周期内做匀变速运动,加速度的大小为
a=$\frac{q{U}_{0}}{md}$
在第一个半周期内,加速度的与初速度方向相反,若初速度较大,在交流电的半个周期内减速后速度仍大于0,则将一直向一个方向运动直到从B孔射出,则此时的对应的最小入射速度为:vC=a•$\frac{T}{2}$=$\frac{q{U}_{0}}{md}$•$\frac{T}{2}$=$\frac{q{U}_{0}T}{2md}$
微粒加速过程中由动能定理得:
qUc=$\frac{1}{2}$m${v}_{C}^{2}$-0
可解得:Uc=$\frac{q{U}_{0}^{2}{T}^{2}}{8m{d}^{2}}$
(2)当加速电压较小,微粒进入电场的第一个$\frac{T}{2}$时间内,加速度方向与初速度相反,
若初速度v<$\frac{1}{4}$aT,粒子在第一个四分之一周期内速度要减至O,然后反向向A运动,直至退出电场,
即v<$\frac{q{U}_{0}T}{4md}$
微粒要从A孔退出,微粒不能从B孔穿出对应的加速电压:
所以:qU<$\frac{1}{2}$mv2;
即:U<$\frac{m{v}^{2}}{2q}$=$\frac{q{U}_{0}^{2}{T}^{2}}{32m{d}^{2}}$
答:(1)Uc大小为$\frac{q{U}_{0}^{2}{T}^{2}}{8m{d}^{2}}$;
(2)加速电压U<$\frac{q{U}_{0}^{2}{T}^{2}}{32m{d}^{2}}$时,带电粒子恰好返回A孔.
点评 本题关键是掌握带电粒子在电场中做匀变速运动,根据题设要求由运动规律求解出粒子进入电场时的速度与电场强度的关系.掌握规律找出问题的突破口是解决本题的关键.

 阅读快车系列答案
阅读快车系列答案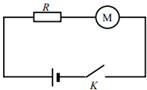 如图所示,一个电阻R和一个电动机M串联接在电动势为E,内电阻为r的直流电源上,电路中的电流为I,电动机正常转动,电阻R两端的电压为U1,电功率为P1,电动机两端的电压为U2,电功率为P2,则下列关系式正确的是( )
如图所示,一个电阻R和一个电动机M串联接在电动势为E,内电阻为r的直流电源上,电路中的电流为I,电动机正常转动,电阻R两端的电压为U1,电功率为P1,电动机两端的电压为U2,电功率为P2,则下列关系式正确的是( )| A. | P1=EI | B. | P2=U2I | C. | U1=E•Ir | D. | U2=IR |
| A. | 第2s的平均速度为15m/s | |
| B. | 后一秒的位移总比前一秒的位移多5m | |
| C. | 前 一秒的平均速度总比后一秒的平均速度小10m/s | |
| D. | 第7s的位移为65m |
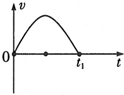
| A. | 质点的速度先减小后增大 | |
| B. | 质点在t1时刻离开出发点最远 | |
| C. | 质点运动的加速度先减小后增大 | |
| D. | 图中正弦曲线是质点的实际运动轨迹 |
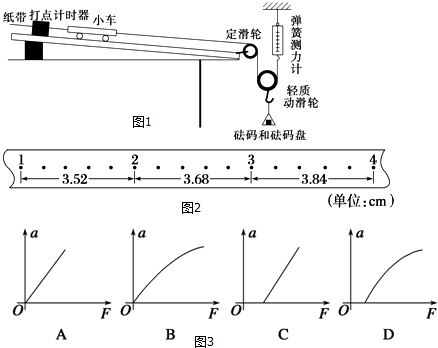
 如图所示,两个高1.2m左右的支架上,放着两条平行光滑铝合金导轨,且已调成水平状态,在光滑的导轨上放着两辆质量相等、性质一样的小车,1号车放在左端,系有一根通过木板右端的小定滑轮的细线,线端有一小桶,桶中可放砝码.2号车放在右端,系有一根通过木板左端的小定滑轮的细线,线端有一相同的小桶,两辆车一开始被左、右两端的电磁铁吸住,电磁铁串联后接在6V的学生电源上(闭合),断开电源,电磁铁同时失去磁性,小车在拉力作用下从两端向中间运动,在某位置相碰,记下相碰位置,可以通过木板上的刻度知道两车通过的位移x1、x2.比较两车的位移x就可比较两车的加速度a,则两车加速度$\frac{{a}_{1}}{{a}_{2}}$=$\frac{{x}_{1}}{{x}_{2}}$.
如图所示,两个高1.2m左右的支架上,放着两条平行光滑铝合金导轨,且已调成水平状态,在光滑的导轨上放着两辆质量相等、性质一样的小车,1号车放在左端,系有一根通过木板右端的小定滑轮的细线,线端有一小桶,桶中可放砝码.2号车放在右端,系有一根通过木板左端的小定滑轮的细线,线端有一相同的小桶,两辆车一开始被左、右两端的电磁铁吸住,电磁铁串联后接在6V的学生电源上(闭合),断开电源,电磁铁同时失去磁性,小车在拉力作用下从两端向中间运动,在某位置相碰,记下相碰位置,可以通过木板上的刻度知道两车通过的位移x1、x2.比较两车的位移x就可比较两车的加速度a,则两车加速度$\frac{{a}_{1}}{{a}_{2}}$=$\frac{{x}_{1}}{{x}_{2}}$.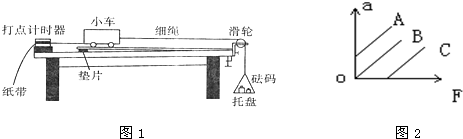
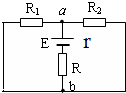 如图所示,电源电动势E=8V,内阻r=1Ω,R1=R2=R3=2Ω,求:
如图所示,电源电动势E=8V,内阻r=1Ω,R1=R2=R3=2Ω,求: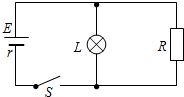 如图所示,电源电动势E=10V,内阻r=0.5Ω,标有“8V,16W”字样的灯泡恰好正常发光,求:
如图所示,电源电动势E=10V,内阻r=0.5Ω,标有“8V,16W”字样的灯泡恰好正常发光,求: