题目内容
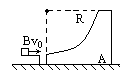
如下图所示，质量为M的物体A静止在光滑水平面上，它有一个位于竖直平面内的光滑轨道，轨道为半径是R的1/4圆弧，底端与水平方向相切，另一质量为m的小物体B从左边以初速度v0滑到光滑轨道的底端，并从轨道顶端冲出．B离开轨道之后，还能不能落回到A的轨道上？如果不能，说明理由；如果能，请计算从B离开轨道到落回轨道这段时间内，A在桌面上滑行的距离．
答案：
解析：
解析：
|
B与A的相互作用过程中，水平方向动量守恒，设B离开A时刻，共同的水平速度为v1， ∴ mv0＝(M＋m)v1 同时A、B系统机械能守恒，设B离开A时刻，B的竖直分速度为v2，则 解出
v1＝ 由于B离开A后与A具有相同的水平速度，因此能落回A的轨道上，从B离开A到落回A，B运动的总时间
t＝ ∴A移动的距离 s＝ |
，v2＝
，
＝
练习册系列答案
名校课堂系列答案
相关题目
如下图所示，质量为m，电量为e的电子，从A点以速度v0垂直场强方向射入匀强电场中，从B点射出电场时的速度方向与电场线成120度角，则A、B两点间的电势差是多少？
C.F2=mgcosθ D.F2=
B.
D.
