题目内容
如下图所示,质量为M、长度为l的小车静止在光滑的水平面上.质量为m的小物块(可视为质点)放在小车的最左端.现用一水平恒力F作用在小物块上,使小物块从静止开始做匀加速直线运动.小物块和小车之间的摩擦力为Ff,小物块滑到小车的最右端时,小车运动的距离为x,在这个过程中,以下结论正确的是( )

A.小物块到达小车最右端时具有的动能为F(l+x)
B.小物块到达小车最右端时,小车具有的动能为Ffx
C.小物块克服摩擦力所做的功为Ffl
D.小物块和小车增加的机械能为Fx
【答案】
B
【解析】
试题分析:对物块分析,物块的位移为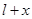 ,根据动能定理得,
,根据动能定理得,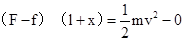 ,则知物块到达小车最右端时具有的动能为
,则知物块到达小车最右端时具有的动能为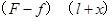 .故A错误.对小车分析,小车的位移为l,根据动能定理得,
.故A错误.对小车分析,小车的位移为l,根据动能定理得,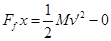 ,知物块到达小车最右端时,小车具有的动能为
,知物块到达小车最右端时,小车具有的动能为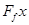 .故B正确.物块相对于地的位移大小为
.故B正确.物块相对于地的位移大小为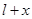 ,则物块克服摩擦力所做的功为
,则物块克服摩擦力所做的功为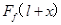 .故C错误.根据能量守恒得,外力F做的功转化为小车和物块的机械能和摩擦产生的内能,则有:
.故C错误.根据能量守恒得,外力F做的功转化为小车和物块的机械能和摩擦产生的内能,则有: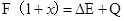 ,则物块和小车增加的机械能为
,则物块和小车增加的机械能为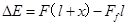 .故D错误.
.故D错误.
故选B
考点:动能定理的应用;功能关系.
点评:本题关键是灵活地选择研究对象进行受力分析,再根据动能定理列式后分析求解.

练习册系列答案
相关题目
 如下图所示,质量为m,电量为e的电子,从A点以速度v0垂直场强方向射入匀强电场中,从B点射出电场时的速度方向与电场线成120度角,则A、B两点间的电势差是多少?
如下图所示,质量为m,电量为e的电子,从A点以速度v0垂直场强方向射入匀强电场中,从B点射出电场时的速度方向与电场线成120度角,则A、B两点间的电势差是多少?