题目内容
【题目】如图所示，在粗糙水平台阶上静止放置一质量m＝0.5kg的小物块，它与水平台阶表面间的动摩擦因数
＝0.5，且与台阶边缘O点的距离s＝5m。在台阶右侧固定了一个以O点为圆心的圆弧形挡板，现用F＝5N的水平恒力拉动小物块，一段时间后撤去拉力，小物块最终水平抛出并击中挡板。（g取10m/s2）
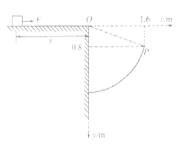
（1）若小物块恰能击中挡板的上边缘P点，P点的坐标为（1.6m，0.8m），求其离开O点时的速度大小；
（2）为使小物块击中挡板，求拉力F作用的距离范围；
【答案】（1）
; （2）
【解析】
(1) 小物块从O到P做平抛运动，水平方向
x=v0t
竖直方向
解得：
v0=4m/s
(2) 为使小物块击中档板,小物块必须能运动到O点,设拉力F作用的最短距离为x1,由动能定理得:
计算得出:
为使小物体不会飞出档板,小物块的平抛初速度不能超过
;设拉力F作用的最长距离为x2,由动能定理可得:
计算得出:
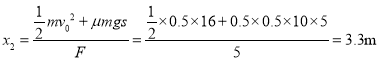
故为使物块击中档板,拉力F的作用距离范围为:
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
