题目内容
4. 某静电场方向平行于x轴,其电势φ随x的分布可简化为如图所示的折线.一个带负电的粒子(忽略重力)在电场中以x=0为中心、沿x轴方向做周期性运动.取x轴正方向为电场强度E、粒子加速度a、速度.的正方向,下图分别表示x轴上各点的电场强度E、粒子的加速度a.速度v和动能Ek随x的变化图象,其中可能正确的是( )
某静电场方向平行于x轴,其电势φ随x的分布可简化为如图所示的折线.一个带负电的粒子(忽略重力)在电场中以x=0为中心、沿x轴方向做周期性运动.取x轴正方向为电场强度E、粒子加速度a、速度.的正方向,下图分别表示x轴上各点的电场强度E、粒子的加速度a.速度v和动能Ek随x的变化图象,其中可能正确的是( )| A. |  | B. |  | C. | 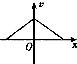 | D. |  |
分析 在φ-x图象的斜率表示电场强度,判断出场强的大小,由牛顿第二定律F=qE=ma判断出加速度的变化,由v=v0+at判断出速度的变化,根据动能定理判断出动能的变化
解答 解:A、φ-x图象的斜率表示电场强度,沿电场方向电势降低,因而在x=0的左侧,电场向左,且为匀强电场,故A 错误;
B、由于离子带负电,粒子在x=0的左侧加速度为正值,在x=0右侧加速度为负值,且大小不变,故B错误;
C、在x=0左侧粒子向右匀加速,在x=0的右侧向右做匀减速运动,速度与位移不成正比,故C错误;
D、在x=0左侧粒子根据动能定理qEx=Ek2,在x=0的右侧,根据动能定理可得-qEx=Ek′-Ek,故D正确
故选:D
点评 本题主要考查了φ-x图象,从图象中判断出斜率即为电场强度,然后利用牛顿第二定律判断出加速度,速度时间公式判断速度,抓住粒子带负电即可

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
15.两个球形行星A和B各有一颗靠近表面的卫星a和b.若这两颗卫星的周期之比Ta:Tb=p,半径之比RA:RB=q,则此两个行星的质量之比MA:MB为( )
| A. | $\frac{q}{p}$ | B. | $\sqrt{\frac{q}{p}}$ | C. | $\frac{{q}^{2}}{{p}^{3}}$ | D. | $\frac{{q}^{3}}{{p}^{2}}$ |
12. 如图所示,一只小球悬挂在弹簧的下端,现用手将小球向下拉一小段位移后释放,便可看到小球做上下的振动.当小球振动到达最高点时,弹簧( )
如图所示,一只小球悬挂在弹簧的下端,现用手将小球向下拉一小段位移后释放,便可看到小球做上下的振动.当小球振动到达最高点时,弹簧( )
 如图所示,一只小球悬挂在弹簧的下端,现用手将小球向下拉一小段位移后释放,便可看到小球做上下的振动.当小球振动到达最高点时,弹簧( )
如图所示,一只小球悬挂在弹簧的下端,现用手将小球向下拉一小段位移后释放,便可看到小球做上下的振动.当小球振动到达最高点时,弹簧( )| A. | 一定是处于拉伸状态 | B. | 一定是处于压缩状态 | ||
| C. | 一定是处于原长状态 | D. | 三种情况都有可能 |
19. 1913年美国物理学家密立根设计了著名的油滴实验,首先直接测定了基元电荷的量值.其模型简化如图,平行板电容器两极板M、N相距d,两极板分别与电压为U的恒定电源两极连接,极板M带正电.现有一质量为m的带电油滴在极板中央处于静止状态,且此时极板带电荷量与油滴带电荷量的比值为k,则( )
1913年美国物理学家密立根设计了著名的油滴实验,首先直接测定了基元电荷的量值.其模型简化如图,平行板电容器两极板M、N相距d,两极板分别与电压为U的恒定电源两极连接,极板M带正电.现有一质量为m的带电油滴在极板中央处于静止状态,且此时极板带电荷量与油滴带电荷量的比值为k,则( )
 1913年美国物理学家密立根设计了著名的油滴实验,首先直接测定了基元电荷的量值.其模型简化如图,平行板电容器两极板M、N相距d,两极板分别与电压为U的恒定电源两极连接,极板M带正电.现有一质量为m的带电油滴在极板中央处于静止状态,且此时极板带电荷量与油滴带电荷量的比值为k,则( )
1913年美国物理学家密立根设计了著名的油滴实验,首先直接测定了基元电荷的量值.其模型简化如图,平行板电容器两极板M、N相距d,两极板分别与电压为U的恒定电源两极连接,极板M带正电.现有一质量为m的带电油滴在极板中央处于静止状态,且此时极板带电荷量与油滴带电荷量的比值为k,则( )| A. | 油滴带正电 | |
| B. | 油滴带电荷量为$\frac{mg}{Ud}$ | |
| C. | 电容器的电容为$\frac{kmgd}{U^2}$ | |
| D. | 将极板N向下缓慢移动一小段距离,油滴将向上运动 |
16. 一矩形线圈绕垂直于匀强磁场方向、并位于线圈平面内的固定轴转动,线圈中的感应电动势e随时间t的变化情况如图所示,则( )
一矩形线圈绕垂直于匀强磁场方向、并位于线圈平面内的固定轴转动,线圈中的感应电动势e随时间t的变化情况如图所示,则( )
 一矩形线圈绕垂直于匀强磁场方向、并位于线圈平面内的固定轴转动,线圈中的感应电动势e随时间t的变化情况如图所示,则( )
一矩形线圈绕垂直于匀强磁场方向、并位于线圈平面内的固定轴转动,线圈中的感应电动势e随时间t的变化情况如图所示,则( )| A. | t1时刻穿过线圈的磁通量为零 | |
| B. | t2时刻穿过线圈的磁通量为零 | |
| C. | t3时刻穿过线圈的磁通量变化率为零 | |
| D. | t4时刻穿过线圈的磁通量变化率为零 |
14. 一物体悬挂在细绳下端,由静止开始沿竖直方向向下运动,运动的过程中,物体的机械能E随位移S变化图象如图所示,其中ab段图线为曲线,bc段图线为直线,则下面判断正确的是( )
一物体悬挂在细绳下端,由静止开始沿竖直方向向下运动,运动的过程中,物体的机械能E随位移S变化图象如图所示,其中ab段图线为曲线,bc段图线为直线,则下面判断正确的是( )
 一物体悬挂在细绳下端,由静止开始沿竖直方向向下运动,运动的过程中,物体的机械能E随位移S变化图象如图所示,其中ab段图线为曲线,bc段图线为直线,则下面判断正确的是( )
一物体悬挂在细绳下端,由静止开始沿竖直方向向下运动,运动的过程中,物体的机械能E随位移S变化图象如图所示,其中ab段图线为曲线,bc段图线为直线,则下面判断正确的是( )| A. | 0-s1过程中物体所受的拉力一定是变力,且不断减小 | |
| B. | s1-s2过程中物体一定做匀速直线运动 | |
| C. | s1-s2过程中物体可能做匀加速直线运动 | |
| D. | s1-s2过程中物体的动能可能在不断增大 |
 如图所示,粗糙的水平面上静止放置三个质量均为m的小木箱,相邻两小木箱的距离均为l.工人用沿水平方向的力推最左边的小术箱使之向右滑动,逐一与其它小木箱碰撞.每次碰撞后小木箱都牯在一起运动.整个过程中工人的推力不变,最后恰好能推着兰个木箱匀速运动.已知小木箱与水平面间的动摩擦因数为μ,重力加速度为g.设碰撞时间极短,小木箱可视为质点.求:第一次碰撞和第二次碰撞中木箱损失的机械能之比.
如图所示,粗糙的水平面上静止放置三个质量均为m的小木箱,相邻两小木箱的距离均为l.工人用沿水平方向的力推最左边的小术箱使之向右滑动,逐一与其它小木箱碰撞.每次碰撞后小木箱都牯在一起运动.整个过程中工人的推力不变,最后恰好能推着兰个木箱匀速运动.已知小木箱与水平面间的动摩擦因数为μ,重力加速度为g.设碰撞时间极短,小木箱可视为质点.求:第一次碰撞和第二次碰撞中木箱损失的机械能之比.