��Ŀ����
����Ŀ��һ������ϸ������ѭ���˶��ɣ�ԭ��Ϊl������ϵ��Ϊk������һ�˴���һ���⻬С��O������ˮƽ�����ϵ�ͶӰ��ΪO������ϵ��һ������Ϊm�Ļ���A�ϣ�A����ˮƽ�����ϣ�С��O�����̶��˵���ֱ����Ϊl����ˮƽ����߶�Ϊh��h��mg/k��������A��ˮƽ���������Ħ����Ϊ��ѹ���Ħ̱����ʣ�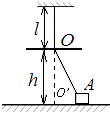
��1����������O�������Ϊrʱ������ϸ���Ի���A������Ϊ���
��2�����鴦��������������ʱ���Ա��־�ֹ״̬��
���𰸡�
��1��
�⣺�Ӽ��ι�ϵ����������ϸ�����쳤��Ϊ��x= ![]()
����ϸ���Ի���A������ΪFT=k��x=k ![]()
��2��
�⣺��A��ֹʱ��O��ľ���Ϊr����λ�ô�A���ܵ��ĸ�����������ͼ��
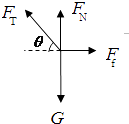
��FT�����ֽ⣬���ڴ���ƽ��״̬�����У�
��ֱ����FN+FTsin��=mg��
ˮƽ����FTcos��=Ff
��FT=k ![]() ��Ffmax=��FN
��Ffmax=��FN
������k ![]() cos��=f��fmax=�� ��mg��kh��
cos��=f��fmax=�� ��mg��kh��
���� ![]() cos��=r
cos��=r
�� ![]()
�������������Ծ�ֹ����O��ΪԲ�ģ� ![]() Ϊ�뾶��Բ���ڵ�����λ��
Ϊ�뾶��Բ���ڵ�����λ��
������������ϸ������ѭ���˶��ɣ��ڵ������ڣ��ܵ����������쳤�������ȣ�
�Ի�����������������ƽ��״̬���������Ħ����֪ʶ������⣮
�����㾫�������þ�Ħ��������Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪��Ħ����:��Ħ������С����0��fmax ֮��仯��һ��Ӧ����������˶�״̬��ƽ��������ţ�ٶ�������⣮