题目内容
【题目】如图所示，在水平面上有一弹簧，其左端与墙壁相连，O点为弹簧原长位置，O点左侧水平面光滑，水平段OP长L＝1 m，P点右侧一与水平方向成θ＝30°的足够长的传送带与水平面在P点平滑连接，皮带轮逆时针转动速率为3 m/s，一质量为1 kg可视为质点的物块A压缩弹簧(与弹簧不拴接)，使弹簧获得弹性势能Ep＝9 J，物块与OP段动摩擦因数μ1＝0.1，另一与A完全相同的物块B停在P点，B与传送带间的动摩擦因数μ2＝
，传送带足够长，A与B的碰撞时间不计，碰后A、B交换速度，重力加速度g取10 m/s2，现释放A，求：
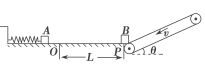
(1)物块A、B第一次碰撞前瞬间，A的速度v0；
(2)从A、B第一次碰撞后到第二次碰撞前，B与传送带之间由于摩擦而产生的热量；
(3)A、B能够碰撞的总次数。
【答案】 (1)4 m/s (2)12.25 J (3)6次
【解析】(1)设物块质量为m，A与B第一次碰撞前的速度为v0，
则Ep＝
m
＋μ1mgL，
解得v0＝4 m/s.
(2)设A、B第一次碰撞后的速度分别为vA、vB，则vA＝0，vB＝4 m/s，碰后B沿传送带向上做匀减速运动直至速度为零，加速度大小设为a1，
则mgsin θ＋μ2mgcos θ＝ma1，
解得a1＝gsin θ＋μ2gcos θ＝10 m/s2.
运动的时间t1＝
＝0.4 s，位移x1＝
t1＝0.8 m.
此过程相对运动路程Δs1＝vt1＋x1＝2 m.
此后B反向加速，加速度仍为a1，由于mgsin θ＝μ2mgcos θ，B与传送带共速后做匀速运动直至与A再次碰撞，
加速时间为t2＝
＝0.3 s，
位移为x2＝
t2＝0.45 m.
此过程相对运动路程Δs2＝vt2－x2＝0.45 m.
全过程摩擦产生的热量Q＝μ2mg(Δs1＋Δs2)cos θ＝12.25 J.
(3)B与A第二次碰撞，两者速度再次互换，此后A向左运动再返回与B碰撞，B沿传送带向上运动再次返回，每次碰后到再次碰前速率相等，重复这一过程直至两者不再碰撞，则对A、B和弹簧组成的系统，从第二次碰撞后到不再碰撞满足
mv2＝2nμ1mgL.
解得第二次碰撞后重复的过程数为n＝2.25，所以碰撞总次数为N＝2＋2n＝6.5＝6(取整数)．
