题目内容
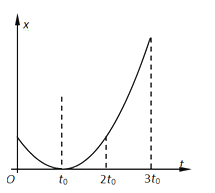
【题目】某质点在同一直线上运动时的位移—时间(x-t)图象为一抛物线,这条抛物线关于t=t0对称,点(t0,0)为抛物线的顶点。下列说法正确的是
A. 该质点在0—3t0的时间内运动方向保持不变
B. 在t0时刻,质点的加速度为零
C. 在0—3t0的时间内,速度先减小后增大
D. 质点在0—t0、t0—2t0、2t0—3t0三个相等时间段内通过的位移大小之比为1:1:4
【答案】C
【解析】由图可知,开始时质点运动的方向与选取的正方向相反,后运动的方向与选取的正方向相同.故A错误;由于质点的位移-时间(x-t)图象为一抛物线,可知质点的加速度保持不变,所以在t0时刻,质点的加速度不为零.故B错误;由于图象的斜率表示速度,由图可知,在0-3t0的时间内,速度先减小后增大.故C正确;由于质点的位移-时间(x-t)图象为一抛物线,结合图象 的特点可得:x=k(tt0)2
在t=0时刻:x0=kt02
在t=t0时刻:x1=0
在t=2t0时刻:x2=k(2t0t0)2=k t02
在t=3t0时刻:x3=k(3t0t0)2=4k t02
所以质点在0-t0时间内的位移大小:|x10|=|x1x0|=k t02
在t0-2t0时间内的位移:x21=x2x1=k t02
在2t0-3t0时间内的位移:x32=x3x2=3k t02
所以质点在0-t0、t0-2t0、2t0-3t0三个相等时间段内通过的位移大小之比为1:1:3.故D错误.
故选C

练习册系列答案
相关题目