Question

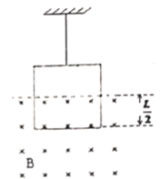
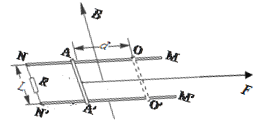
【题目】如图所示，宽L=2m、足够长的金属导轨MN和M′N′固定在水平面上，在导轨的两端各连接一个R=2.0Ω的定值电阻（右端没有画出），在AA′处放置一根与导轨垂直、质量m=2.0kg、电阻r=1.0Ω的金属杆，金属杆与导轨之间的动摩擦因数为0.5，导轨电阻不计，导轨处于磁感应强度B=1.0T、方向垂直于导轨平面向上的匀强磁场中。用轻绳与杆的中点相连，轻绳沿水平方向，用外力牵引杆由AA′处经时间t=2S运动到OO′处，外力的功率恒为P=60W，当杆运动到OO′时速度大小为5m/s，AA′与OO′之间的距离d=4m，g取10m/s2。求：

（1）当杆运动到OO′时，流过杆的电流大小及方向

（2）杆由AA′处运动到OO′处过程中，一个定值电阻R的平均发热功率

Answer 1

【答案】（1）I=5A，电流方向由O到O′ （2）6.875W

【解析】

（1）根据E=BLv求解感应电动势，结合欧姆定律求解电流；根据动能定理求解总热量，然后求解一个定值电阻R的平均发热功率.

（1）杆产生的电动势为 E=BLv

电路中的总电阻为

流过杆的电流为

代入数据解得 I=5A，电流方向由O到O′

（2）对杆根据动能定理有

安培力所做的功全部转化成整个回路的焦耳热，Q=W安

由焦耳定律有

一个定值电阻R的发热功率

代入数据解得 PR= 6.875W