题目内容
14.地球赤道上的物体随地球自转的向心加速度为a1,第一宇宙速度为v1,地球半径为R,同步卫星离地心距离为r,运行速率为v2,向心加速度为a2,则( )| A. | ${a_1}:{a_2}={r^2}:{R^2}$ | B. | a1:a2=r:R | C. | v1:v2=r:R | D. | ${v_1}:{v_2}=\sqrt{r}:\sqrt{R}$ |
分析 同步卫星的周期与地球的自转周期、角速度均相等,根据a=rω2得出同步卫星和随地球自转物体的向心加速度之比;根据万有引力提供向心力得出第一宇宙速度与同步卫星的速度之比.
解答 解:AB、赤道上的物体与同步卫星的角速度相等,根据a=ω2r,有:${a}_{1}:{a}_{2}={ω}^{2}R:{ω}^{2}r=R:r$;故A错误,B错误;
CD、根据万有引力等于向心力,有:$G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}$,得到v=$\sqrt{\frac{GM}{r}}$∝$\frac{1}{\sqrt{r}}$,故${v}_{1}:{v}_{2}=\frac{1}{\sqrt{R}}:\frac{1}{\sqrt{r}}=\sqrt{r}:\sqrt{R}$,故C错误,D正确;
故选:D
点评 解决本题的关键知道同步卫星和随地球自转的物体角速度相等,同步卫星以及贴近地球表面运行的卫星靠万有引力提供向心力.

练习册系列答案
相关题目
4.下列叙述中正确的有( )
| A. | 导体中电荷运动就形成电流 | |
| B. | 电流强度的单位是安培,是国际单位制中的基本单位 | |
| C. | 电流强度是一个标量,其方向是没有意义的 | |
| D. | 对于导体,只要其两端电势差为零,电流强度未必为零 |
2.关于电流通过导体产生的热量的规律描述错误的是( )
| A. | 与电流的二次方成正比 | B. | 与导体的电阻成正比 | ||
| C. | 与电流的大小成正比 | D. | 与通电时间成正比 |
9.关于自由落体运动,下列说法正确的是( )
| A. | 开始下落时,速度、加速度均为零 | B. | 开始下落时,速度为零、加速度为g | ||
| C. | 下落过程中,速度、加速度都增大 | D. | 下落过程中,速度、加速度都减小 |
19.在“描绘小灯泡的伏安特性曲线”实验中,需测量一个标有“3V,1.5W”灯泡两端的电压和通过灯泡的电流.某同学连好的实物图如图甲所示.

(1)在以下电流表中选择合适的一个是B;
A.电流表A1(量程3A,内阻约0.1Ω);
B.电流表A2(量程600mA,内阻约0.5Ω);
C.电流表A3(量程100mA,内阻约3Ω)
(2)该同学连接电路后检查所有元器件都完好,电流表和电压表已调零,经检查各部分接触良好.但闭合开关后,反复调节滑动变阻器,小灯泡的亮度发生变化,但电压表和电流表示数不能调为零,则断路的导线为h;
(3)实验测得的部分数据如表,其I-U图象如图乙所示;
若将该灯泡与一个4Ω的定值电阻串联,直接接在电动势为2V,内阻不计的电源两端,请估算该小灯泡的实际功率P=0.25W (保留两位有效数字).

(1)在以下电流表中选择合适的一个是B;
A.电流表A1(量程3A,内阻约0.1Ω);
B.电流表A2(量程600mA,内阻约0.5Ω);
C.电流表A3(量程100mA,内阻约3Ω)
(2)该同学连接电路后检查所有元器件都完好,电流表和电压表已调零,经检查各部分接触良好.但闭合开关后,反复调节滑动变阻器,小灯泡的亮度发生变化,但电压表和电流表示数不能调为零,则断路的导线为h;
(3)实验测得的部分数据如表,其I-U图象如图乙所示;
| 电压U/V | 0.40 | 0.80 | 1.20 | 1.60 | 2.00 | 2.40 |
| 电流I/A | 0.12 | 0.21 | 0.28 | 0.34 | 0.38 | 0.43 |
6.使两个完全相同的金属小球(均可视为点电荷)分别带上3Q和5Q的电荷后,将它们固定在相距为a的两点,它们之间吸引力的大小为F1.现用绝缘工具使两小球相互接触后,再将它们固定在相距为2a的两点,它们之间库仑力的大小为F2.则F1与F2之比为( )
| A. | 2:1 | B. | 15:4 | C. | 16:1 | D. | 60:1 |
3.下列说法中正确的是( )
| A. | 条形磁铁和蹄形磁铁的内部磁感线都是从磁铁的南极到北极 | |
| B. | 直线电流产生的磁场的磁感线是以导线上的点为圆心的一系列同心圆.该圆的平面与导线垂直 | |
| C. | 把安培定则用于通电螺线管时,大拇指所指的方向是螺线管外部磁感线的方向 | |
| D. | 把安培定则用于环形导线时,当右手弯曲的四指和环形电流方向一致时,大拇指所指的方向是环形导线中心轴线上的磁感线方向 |
1.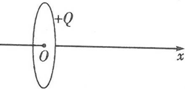 如图所示,一圆环上均匀分布着正电荷,x轴垂直于环面且过圆心O.下列关于X轴上的电场强度和电势的说法中正确的是( )
如图所示,一圆环上均匀分布着正电荷,x轴垂直于环面且过圆心O.下列关于X轴上的电场强度和电势的说法中正确的是( )
 如图所示,一圆环上均匀分布着正电荷,x轴垂直于环面且过圆心O.下列关于X轴上的电场强度和电势的说法中正确的是( )
如图所示,一圆环上均匀分布着正电荷,x轴垂直于环面且过圆心O.下列关于X轴上的电场强度和电势的说法中正确的是( )| A. | O点的电场强度为零,电势最低 | |
| B. | O点的电场强度为零,电势最高 | |
| C. | 从O点沿X轴正方向,电场强度减小,电势减小 | |
| D. | 从O点沿X轴正方向,电场强度先增大后减小,电势一直降低 |
