题目内容
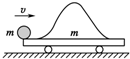
相隔一定距离的A、B两球,质量均为m,假设它们之间存在恒定斥力作用,原来两球被按住,处于静止状态.现突然松开两球,同时给A球以速度v0,使之沿两球连线射向B球,而B球初速为零.设轨道光滑,若两球间的距离从最小值(两球未接触)到刚恢复到原始值所经历的时间为t,求两球间的斥力.
小球运动过程示意图如图所示:

当A、B相距最近时,二者速度应相等,设为v,当二者距离恢复原始值时,设A、B的速度分别为v1、v2,整个过程经历的时间为t′.?
对B球,由动量定理得:Ft=mv2-mv ①
以A、B两球组成的系统为研究对象,系统动量守恒,以A的初速度方向为正方向,
由动量守恒定律得:
从开始到距离最小过程中:mv0=2mv ②
从距离最小到恢复到原始值过程中,mv0=mv1+mv2 ③
整个过程中A、B两球对地的位移相等,则:
t′=
t′④
联立①~④式解得:F=
⑤;
答:两球间的斥力为
.

当A、B相距最近时,二者速度应相等,设为v,当二者距离恢复原始值时,设A、B的速度分别为v1、v2,整个过程经历的时间为t′.?
对B球,由动量定理得:Ft=mv2-mv ①
以A、B两球组成的系统为研究对象,系统动量守恒,以A的初速度方向为正方向,
由动量守恒定律得:
从开始到距离最小过程中:mv0=2mv ②
从距离最小到恢复到原始值过程中,mv0=mv1+mv2 ③
整个过程中A、B两球对地的位移相等,则:
| v0+v1 |
| 2 |
| v2 |
| 2 |
联立①~④式解得:F=
| mv0 |
| 2t |
答:两球间的斥力为
| mv0 |
| 2t |

练习册系列答案
相关题目