题目内容
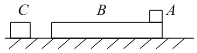
【题目】如图所示,在光滑桌面上置有长木板B和物块C,在长木板的右侧置有物块A,一开始A.B处于静止状态。物块A与长木板B之间的动摩擦因数为0.2,长木板B足够长。物块A的质量为2kg,长木板B的质量为1kg,物块C的质量为3kg.物块C以4m/s的初速度向右运动,与长木板B碰撞后,与长木板B黏在一起。重力加速度g取10m/s2,试求:
(1)C与B碰撞过程中,损失的机械能;
(2)最终A. B.C的速度大小和A相对于B运动的距离。
【答案】(1) ![]() (2)
(2) ![]()
【解析】(1)对于C与B碰撞的过程,取向右为正方向,根据动量守恒定律得:
mCv0=(mC+mB)v1.
可得![]()
C与B碰撞过程中,损失的机械能![]() ;
;
解得△E=6J
(2)由于木板B足够长,所以最终三者速度相同,取向右为正方向,由动量守恒定律得:
mCv0=(mA+mC+mB)v2.
代入数据解得v2=2m/s
对系统运用能量守恒定律得:
μmAgd=![]() (mC+mB)v12
(mC+mB)v12![]() (mA+mC+mB)v22.
(mA+mC+mB)v22.
代入数据解得A相对于B运动的距离d=1.5m.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目