题目内容
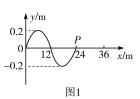
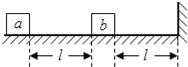
【题目】如图甲所示,足够长的木板C通过某一装置锁定在地面上,物块A、B静止在木板C上,物块A、B间距离为1.1m。开始时物块A以速度v0=6m/s向右运动,物块A在与B碰撞前一段时间内的运动图像如图乙所示。已知物块A、B可视为质点,质量分别为mA=1kg、mB=4kg,A、B与木板间的动摩擦因数相同,木板C的质量mC=1kg,C与地面间的动摩擦因数为![]() 。A与B弹性碰撞过程时间极短、可忽略摩擦力的影响,A、B碰撞瞬间木板C解除锁定。重力加速度取10m/s2。求:
。A与B弹性碰撞过程时间极短、可忽略摩擦力的影响,A、B碰撞瞬间木板C解除锁定。重力加速度取10m/s2。求:

(1)物块与木板间的动摩擦因数;
(2)碰撞后瞬间物块A的速度;
(3)最后停止时物块A、B间的距离(结果保留两位小数)。
【答案】(1)0.5(2) 3m/s,方向向左(3)1.37m
【解析】
根据图像可知![]() ①
①
对A受力分析并列牛顿第二定律:![]() ②
②
联立①②式解得物块与木板间的动摩擦因数![]() ③
③
(2)设碰撞前瞬间A的速度为v,则
![]() ④
④
由于A、B弹性碰撞,碰撞后A、B的速度分别为vA、vB,取向右为正方向,则
![]() ⑤
⑤
![]() ⑥
⑥
联立④⑤⑥式解得:vA=-3m/s、vB=2m/s;即碰撞后瞬间物块A的速度大小为3m/s,方向向左。⑦
(3)碰撞后对木板C受力分析得![]() ⑧
⑧
由物块B受力得:![]() ⑨
⑨
设经时间t1物块B与木板C达到相同的速度v,则![]() ⑩
⑩
此时C的速度为![]()
联立⑧⑨⑩解得:![]()
从碰撞结束到B、C速度相同,B向右的位移大小为x2,则
![]()
B、C相对静止后一起运动,设其加速度为a,则![]()
B、C一起向右运动的位移大小为x3,则![]()
A碰撞后到停下经过的位移大小为x4,则![]()
最后停止时物块A、B间的距离![]()

练习册系列答案
相关题目