题目内容
【题目】有一架电梯,启动时匀加速上升,加速度为2m/s2,制动时匀减速上升,加速度大小为1m/s2,楼高52m.
(1) 求电梯启动后加速到6m/ s时的位移是多大?
(2) 求电梯从启动到速度达到6m/s所用的时间?
(3) 若上升的最大速度为6m/s,电梯升到楼顶的最短时间是多少?
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)根据位移速度公式求出匀加速直线运动的位移;
(2)根据速度时间公式求出匀加速直线运动的时间;
(3)根据速度时间公式求出匀减速直线运动的时间,结合位移公式求出匀减速直线运动的位移,从而得出匀速运动的位移,求出匀速运动的时间,得出运动的总时间;
(1)根据速度与位移关系可以得到电梯启动后加速到![]() 时的位移是:
时的位移是:![]() ;
;
(2)根据速度与时间关系可以得到匀加速上升的时间为:![]() ;
;
(3)根据速度与位移关系可以得到匀减速上升的高度为:![]() ,
,
根据速度与时间关系可以得到匀减速上升的时间:![]()
匀速运动的位移为:![]()
则匀速运动的时间为:![]()
则电梯升到楼顶的最短时间是:![]() 。
。

 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案【题目】为了最大限度地减少道路交通事故,全国开始了“集中整治酒后驾驶违法行为”专项行动.这是因为一般驾驶员酒后的反应时间比正常时慢了0.1~0.5 s,易发生交通事故.图示是《驾驶员守则》中的安全距离图示(如右图所示)和部分安全距离表格.
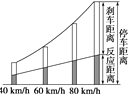
车速 v(km/h) | 反应距离 s(m) | 刹车距离 x(m) | 停车距离 L(m) |
54 | 12 | 10 | 22 |
72 | 16 | 17.8 | 33.8 |
108 | A | B | C |
请根据该图表回答下列问题(结果保留两位有效数字):
(1)请根据表格中的数据计算驾驶员的反应时间.
(2)如果驾驶员的反应时间相同,请计算出表格中A的数据.
(3)假设在同样的路面上,一名饮了少量酒的驾驶员驾车以90 km/h速度行驶,在距离一学校门前50 m处发现有一队学生在斑马线上横过马路,他的反应时间比正常时慢了0.2 s,请用详细计算过程说明会发生交通事故吗?