题目内容
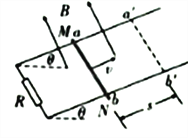
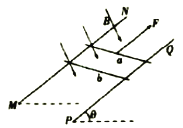
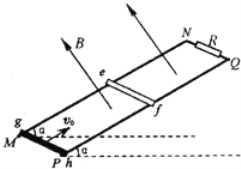
【题目】如图所示，两根平行金属导轨MN、PQ相距d=1.0m，导轨平面与水平面夹角
，导轨上端跨接一定值电阻
，导轨电阻不计。整个装置处于方向垂直导轨平面向上、磁感应强度大小B=1.0T的匀强磁场中，金属棒ef垂直于MN、PQ静止放置，且与导轨保持良好接触，其长度刚好为d、质量
=0.10kg、电阻
，距导轨底端的距离
。另一根与金属棒平行放置的绝缘棒gh长度也为d，质量为
=0.05kg，从轨道最低点以速度
=10m/s沿轨道上滑并与金属棒发生正碰（碰撞时间极短），碰后金属棒沿导轨上滑一段距离后再次静止，此过程中流过金属棒的电荷量q=0.1C且测得从碰撞至金属棒静止过程中金属棒上产生的焦耳热Q=0.05J。已知两棒与导轨间的动摩擦因数均为
，g=10m/s2。求：
（1）碰后金属棒ef沿导轨上滑的最大距离
；
（2）碰后瞬间绝缘棒gh的速度
；
（3）金属棒在导轨上运动的时间Δt。
【答案】（1）
（2）
（3）
【解析】试题分析：根据电磁感应定律求出感应电动势，感应电流，再根据电量的表达式求出运动的位移；根据动能定理和热量分配关系，进而求出绝缘棒的速度；根据动量定理求出金属棒在导轨上运动的时间。
（1）碰后的电动势为： 
回路的电流为： 
通过的电量为： 
磁通量的变化量为：△Φ=Bds2
以上联立解得： 
（2）碰前： 对gh由动能定理： 
代入解得： 
对ef由能量守恒得： 
热量关系为： 
联立以上并代入数据解得： 
相碰时由动量守恒： 
代入数据解得： 
方向沿导轨向下
（3）由动量定理： 
通过的电荷量为： 
联立以上并代入数据解得： 
练习册系列答案
相关题目
