题目内容
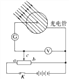
【题目】在如图所示的装置中,离子源A可提供速度很小的正离子(其速度可视为零),经加速电压加速后从S点进入匀强磁场,磁场方向垂直于纸面向外,虚线框为磁场区域的边界线,在磁场作用下,离子沿半个圆周运动后射出磁场,射出点P到S的距离用x表示。
(1)当离子源提供的是单一种类的第一种离子时,P到S的距离为x1,当离子源提供的是单一种类的第二种离子时,P到S的距离为x2,已知x1/x2=a。试求这两种离子在磁场中运动的时间之比。
(2)若离子源A提供的是由H+、D+、4He+、H2+混合而成的多种离子,又通过速度选择器使各种离子的速度的速率都为v,当这些离子从S点进入匀强磁场后,从磁场射出时可分离出哪几种离子束?若v=2.0×106m/s,B=0.50T,元电荷e=1.60×10-19C,质子质量mP=1.68×10-27kg,试求各种离子出点P到S的距离。

【答案】(1)![]() (2)
(2)![]()
![]()
![]()
![]()
【解析】试题分析:对粒子根据动能定理求出速度,在根据洛伦兹力提供向心力,求出半径和周期表达式,根据题意即可解题;x取决于粒子的电荷量与质量的比值,找出这几种粒子的比荷关系即可解题。
(1)设加速电压为U,电量为q,加速后的速度为v,
根据动能定理得: ![]()
粒子进入磁场后。在洛伦兹力的作用下做圆周运动,半径为R,磁感应强度为B.
则有: ![]() 周期为:
周期为: ![]()
设两种粒子的电荷量分别为q1、q2,质量分别为m1、m2,进入磁场的速度分别为v1、v2
根据题意得: ![]()
![]()
![]()
以上联立解得: ![]()
(2)x取决于粒子的电荷量与质量的比值,可以看出氘核(D+)氢分子粒子(H2+)的电荷量与质量的比值相同,他们将从同一点射出磁场,这两种离子束不能被磁场分开,而质子和氦粒子的电荷量与质量的比值不相同,也与氘核和氢分子粒子的不同,他们将从不同点射出磁场,可以单独分离出来,故可获得质子束流、氦离子流、氘核与氢分子粒子混合的束流,共三种束流。把有关数据代入得:
![]()
![]()
![]()
![]()