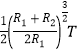题目内容
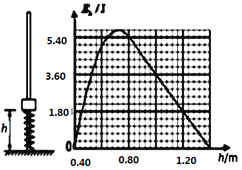
【题目】如图所示，竖直光滑长杆固定不动，套在杆上的轻质弹簧下端固定，套在杆上的滑块质量为0.80 kg，现向下压滑块，至弹簧上端离地高度h=0.40 m处，滑块与弹簧不拴接。现由静止释放滑块，通过传感器测量出滑块的速度和离地高度h，计算出滑块的动能EK，并作出滑块的Ek - h图象，其中高度从0.80 m上升到1.40m范围内图象为直线，其余部分为曲线。若以地面为重力势能的零势能面，空气阻力不能忽略，取g=10 m/s2,则结合图象可知 ( )
A. 空气阻力恒定为1.00N
B. 弹簧原长为0.72 m
C. 弹簧最大弹性势能为9.00 J
D. 滑块的重力势能与弹簧的弹性势能总和最小为3.60J
【答案】AC
【解析】试题分析：根据动能定理分析知道
图象的斜率表示滑块所受的合外力，从而求得空气阻力。高度从0.80m上升到1.40m范围内图象为直线，其余部分为曲线，结合能量守恒定律求解滑块的重力势能与弹簧的弹性势能总和最小值。
在0.80m上升到1.40m内，在
图象中，根据动能定理知：图线的斜率大小表示滑块所受的合外力，由于高度从0.80m上升到1.40m范围内图象为直线，其余部分为曲线，说明滑块从0.80m上升到1.40m范围内所受作用力为恒力，根据动能定理得
，由图知
，解得空气阻力
，A正确；从h=0.8m开始，滑块与弹簧分离，则知弹簧的原长为0.8m，B错误；根据能的转化与守恒可知，当滑块上升至最大高度时，整个过程中，增加的重力势能和克服空气阻力做功之和等于弹簧的最大弹性势能，所以
，C正确；由图可知，当h=0.56m时滑块的动能最大，为Ekm=5.76J；假设空气阻力不计，则在整个运动过程中，系统的动能、重力势能和弹性势能之间相互转化，因此滑块的动能最大时，滑块的重力势能与弹簧的弹性势能总和最小，为
，由于有空气阻力，所以滑块的重力势能与弹簧的弹性势能总和最小小于3.24J，D错误．
