Question

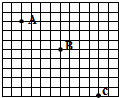在研究平抛运动的实验中，用一张印有小方格的纸记录轨迹，坐标纸上每个小方格边长均为5cm，在坐标纸上的3个位置为a，b，c，抛出点未知，则小球经过B点的速度大小为

2

2

m/s（结果可保留根号）

Answer 1

分析：平抛运动在水平方向上做匀速直线运动，在竖直方向上做自由落体运动，结合竖直方向上相邻相等时间内的位移之差是一恒量求出相等的时间间隔，结合水平位移求出初速度的大小．根据竖直方向上某段时间内的平均速度等于中间时刻的瞬时速度求出B点竖直分速度，结合平行四边形定则求出B点的速度大小．

解答：解：根据yBC-yAB=2L=gT2，
则T=

2L g

=

2×0.05 10

s=0.1s．
则小球的初速度v0=

4L

T

=

0.2

0.1

m/s=2m/s．
小球经过B点竖直方向上的分速度vyB=

8L

2T

=

0.4

0.2

m/s=2m/s．
则B点的速度vB=

v02+vyB2

=2

2

m/s．
故答案为：2

2

点评：解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律，结合运动学公式和推论灵活求解．