题目内容
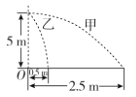
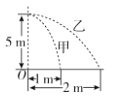
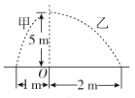
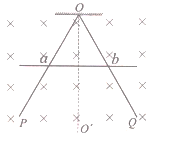
【题目】如图所示，
是折成60°角的固定于竖直平面内的光滑金属导轨，导轨关于竖直轴线
对称，
，整个装置处在垂直导轨平面向里的足够大的匀强磁场中，磁感应强度为
。一质量为
、长为
、电阻为
、粗细均匀的导体棒锁定于
的中点
位置。将导体棒解除锁定，导体棒由静止向下加速运动，离开导轨时的速度为
。导体棒与导轨始终保持良好接触，导轨电阻不计，重力加速度为
，下列说法正确的是
A. 解除锁定后，导体棒向下做匀加速直线运动
B. 解除锁定后，导体棒中电流由
到
C. 导体棒滑到导轨末端时的加速度大小为
D. 导体棒下滑过程中产生的焦耳热为
【答案】BCD
【解析】
根据题图可知，考查了导体棒切割磁感线的问题，根据法拉第电磁感应定律求解电动势的大小，根据欧姆定律求解感应电流的大小，根据安培定则判断感应电流的方向，根据安培力公式求解安培力，利用牛顿第二定律求解加速度a，根据能量守恒求解过程中产生的焦耳热。
A、导体棒在下降的过程中，对ab棒进行受力分析有：
，由于导体棒粗细均匀，设单位长度的电阻为
，则电流
，整理得：
，物体做加速运动，
增大，
也增加，故加速度
在减小，故A错误；
B、解除锁定后，导体棒向下运动，由右手定则得，电流由a到b，故B正确；
C、导体棒滑到导轨末端时，导体棒的有效切割长度
，所以加速度大小为
，故C正确；
D、导体棒下滑过程中，由能量守恒得：
，整理得：
，故D正确。
练习册系列答案
相关题目
