题目内容
7.中心均开有小孔的金属板C、D与边长为d的正方形单匝金属线圈连接,正方形框内有垂直纸面的匀强磁场,大小随时间变化的关系为B=kt(k未知且k>0),E、F为磁场边界,且与C、D板平行.D板正下方分布磁场大小均为B0,方向如图所示的匀强磁场.区域Ⅰ的磁场宽度为d,区域Ⅱ的磁场宽度足够大.在C板小孔附近有质量为m、电量为q的正离子由静止开始加速后,经D板小孔垂直进入磁场区域Ⅰ,不计离子重力.
(1)判断金属板CD之间的电场强度的方向和正方形线框内的磁场方向;
(2)若离子从C板出发,运动一段时间后又恰能回到C板出发点,求离子在磁场中运动的总时间;
(3)若改变正方形框内的磁感强度变化率k,离子可从距D板小孔为2d的点穿过E边界离开磁场,求正方形框内磁感强度的变化率k是多少?
分析 本题(1)的关键是根据楞次定律即可求解;题(2)的关键是画出离子运动的轨迹图,找出圆心,根据几何知识可求出三个轨迹对应的圆心角,即可求解;题(3)的关键是先根据法拉第电磁感应定律求出磁场变化率K,然后画出离子从距D板小孔为2d的点穿过E边界离开磁场时存在两种情况的轨迹图,根据几何知识求出圆的半径,代入即可求解.
解答 解:(1)金属板CD之间的电场强度方向由C垂直指向D,正方形线框内的磁场方向垂直纸面向里.
(2)离子在Ⅰ、Ⅱ区域内作圆周运动,半径均为R,有:${{qv}_{0}^{\;}B}_{0}^{\;}$=$\frac{{mv}_{0}^{2}}{R}$…①
运动周期均为T,有:T=$\frac{2πR}{{v}_{0}^{\;}}$…②
解①②得:T=$\frac{2πm}{{qB}_{0}^{\;}}$…③
由题意知粒子运动轨迹如图(甲),将三个轨迹的圆心连接起来,由几何知识可知,所得三角形为等边三角形,所以离子在磁场中运动的总时间为:t=$2•\frac{\frac{π}{3}}{2π}•T$+$\frac{2π-\frac{π}{3}}{2π}•T$=$\frac{T}{3}+\frac{5T}{6}$=$\frac{7T}{6}$…④
解③④得:t=$\frac{7πm}{3q{B}_{0}^{\;}}$…⑤
(3)单匝圆形线框产生的电动势为U,由法拉第电磁感应定律得:U=$\frac{S△B}{△t}$=K${πd}_{\;}^{2}$…⑥
离子从D板小孔射出速度为V,有动能定理得:qU=$\frac{1}{2}{mv}_{\;}^{2}$…⑦
解①⑥⑦得:K=$\frac{{{qB}_{0}^{2}}_{\;}^{\;}{R}_{\;}^{2}}{2π{md}_{\;}^{2}}$…⑧
离子进入磁场从E边界射出的运动轨迹有两种情况:
(Ⅰ)如果离子从小孔下面离开磁场,运动轨迹与F相切,如图(乙)所示
由几何关系知:R=d…⑨
解⑧⑨得:K=$\frac{{{qB}_{0}^{2}}_{\;}^{\;}}{2πm}$…⑩
(Ⅱ)如果离子从小孔上面离开磁场,如图(乙)所示
由几何关系知:$(R+d)_{\;}^{2}+(2d)_{\;}^{2}=(2R)_{\;}^{2}$…(11)
解⑧(11)得:K=$\frac{25{qB}_{0}^{2}}{18πm}$…(12)
答:(1)金属板CD之间的电场强度方向由C垂直指向D,圆形线框内的磁场方向垂直纸面向里;
(2)离子在磁场中运动的总时间为t=$\frac{7πm}{3q{B}_{0}^{\;}}$;
(3)圆形框内磁感强度的变化率k是$\frac{{{qB}_{0}^{2}}_{\;}^{\;}}{2πm}$或$\frac{25{qB}_{0}^{2}}{18πm}$
点评 该题考查带电粒子在组合场中的运动,遇到带电粒子在有界磁场中的运动问题,一般思路是“画轨迹、定圆心、求半径和圆心角,然后求解”.

 如图所示,等腰直角三角体OCD由不同材料A、B拼接而成,P为两材料在CD边上的交点,且DP>CP.现OD边水平放置,让小物块从静止由C滑到D;然后将OC边水平放置,再让 小物块从静止由D滑到C,小物块两次从顶点滑到P点的时间相同,且滑动过程中三角体与 地面均保持静止,则下列说法中正确的是( )
如图所示,等腰直角三角体OCD由不同材料A、B拼接而成,P为两材料在CD边上的交点,且DP>CP.现OD边水平放置,让小物块从静止由C滑到D;然后将OC边水平放置,再让 小物块从静止由D滑到C,小物块两次从顶点滑到P点的时间相同,且滑动过程中三角体与 地面均保持静止,则下列说法中正确的是( )| A. | A、B两材料的动摩擦因数相同 | |
| B. | 两次滑动中物块到达P点速率相等 | |
| C. | 两次滑动中物块到达底端速率相等 | |
| D. | 两次滑动中物块到达底端摩擦生热不相等 |
 如图所示,空间虚线框内有匀强电场,AA′,BB′,CC′是该电场的三个等势面,相邻等势面间的距离为1cm,其中BB′为零电势能面.一质量为m、带电織为+q的粒子沿AA'方向以初速度v0自图中的P点进入电场,刚好从C′点离开电场.已知PA′=2cm粒子的重力忽略不计.倾说法中正确的是( )
如图所示,空间虚线框内有匀强电场,AA′,BB′,CC′是该电场的三个等势面,相邻等势面间的距离为1cm,其中BB′为零电势能面.一质量为m、带电織为+q的粒子沿AA'方向以初速度v0自图中的P点进入电场,刚好从C′点离开电场.已知PA′=2cm粒子的重力忽略不计.倾说法中正确的是( )| A. | 该粒子在P点时的电势能是2mv02 | |
| B. | 该粒子到达C′点时的速度是$\sqrt{2}$v0 | |
| C. | 该粒子到达C′点时的电势能是mv02 | |
| D. | 该粒子通过等势面BB′时的动能是1.5mv02 |

| A. | 卡文迪许通过扭秤实验,测定出了引力常数 | |
| B. | 奥斯特通过实验研究,发现了电流周围存在电场 | |
| C. | 法拉第通过实验研究,总结出法拉第电磁感应定律 | |
| D. | 牛顿根据理想斜面实验,提出力不是维持物体运动的原因 |
| A. | 两球运动中的加速度相同 | B. | 重力对两球做功相同 | ||
| C. | 空气阻力对两球做功相同 | D. | 动能增加相同 |

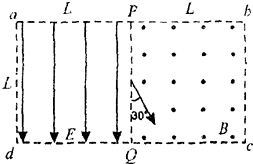 如图所示,虚线框abcd内为边长均为L的正形匀强电场和匀强磁场区域,电场强度的大小为E,方向向下,磁感应强度为B,方向垂直纸面向外,PQ为其分界线,现有一群质量为m,电荷量为-e的电子(重力不计)从PQ中点与PQ成30°.角以不同的初速射入磁场,求:
如图所示,虚线框abcd内为边长均为L的正形匀强电场和匀强磁场区域,电场强度的大小为E,方向向下,磁感应强度为B,方向垂直纸面向外,PQ为其分界线,现有一群质量为m,电荷量为-e的电子(重力不计)从PQ中点与PQ成30°.角以不同的初速射入磁场,求: 如图所示,在xOy坐标系中,以(r,0)为圆心,r为半径的圆形区域内存在匀强磁场磁场区域的圆心为O′,磁场的磁感应强度大小为B,方向垂直于纸面向里.在y>r的足够大的区域内,存在沿y轴负方向的匀强电场,场强大小为E.从O点以相同速率向不同方向发射质子,质子的运动轨迹均在纸面内,且质子在磁场中运动的轨迹半径也为r.已知质子的电荷量为q,质量为m,不计质子所受重与及质子间相互作用力的影响.
如图所示,在xOy坐标系中,以(r,0)为圆心,r为半径的圆形区域内存在匀强磁场磁场区域的圆心为O′,磁场的磁感应强度大小为B,方向垂直于纸面向里.在y>r的足够大的区域内,存在沿y轴负方向的匀强电场,场强大小为E.从O点以相同速率向不同方向发射质子,质子的运动轨迹均在纸面内,且质子在磁场中运动的轨迹半径也为r.已知质子的电荷量为q,质量为m,不计质子所受重与及质子间相互作用力的影响. 2008年9月28日下午五点三十七分,翟志刚、刘伯明、景海鹏三位航天英雄在完成了预定的太空行走、空间科学技术实验等任务后,乘坐宇宙飞船返回舱,顺利返回祖国的怀抱.返回舱开始从太空向地球表面按预定轨道返回,返回舱开始时通过自身制动发动机进行调控减速下降,穿越大气层后,在距地面20km的高度打开降落伞进一步减速下落,到距地面约1m处反冲发动机点火减速,实现软着陆.设返回舱竖直降落,从打开降落伞的时刻开始计时,返回舱运动的v-t图象中的AD曲线所示,图中AB是曲线在A点的切线,切线交于横轴一点B,其坐标为(5,0),CD是曲线AD的渐近线,假如返回舱总质量为M=3000kg,g=10m/s2,
2008年9月28日下午五点三十七分,翟志刚、刘伯明、景海鹏三位航天英雄在完成了预定的太空行走、空间科学技术实验等任务后,乘坐宇宙飞船返回舱,顺利返回祖国的怀抱.返回舱开始从太空向地球表面按预定轨道返回,返回舱开始时通过自身制动发动机进行调控减速下降,穿越大气层后,在距地面20km的高度打开降落伞进一步减速下落,到距地面约1m处反冲发动机点火减速,实现软着陆.设返回舱竖直降落,从打开降落伞的时刻开始计时,返回舱运动的v-t图象中的AD曲线所示,图中AB是曲线在A点的切线,切线交于横轴一点B,其坐标为(5,0),CD是曲线AD的渐近线,假如返回舱总质量为M=3000kg,g=10m/s2,