题目内容
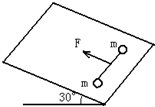 如图所示,两个质量均为m=0.2kg的小球用长L=0.22m的细绳连接,放在光滑水平地面上.初始时刻,细绳处于拉直状态.在绳的中点施加一个大小F=2.2N,方向垂直于绳沿水平向左的恒力,在F作用下两小球开始运动,以后两小球经过若干次碰撞,由于两小球之间有粘性,每一次碰撞后,小球垂直于F方向的速度将减小0.55m/s,当力F作用了2s时,两小球发生了最后一次碰撞,且不再分离.g取10m/s.求:
如图所示,两个质量均为m=0.2kg的小球用长L=0.22m的细绳连接,放在光滑水平地面上.初始时刻,细绳处于拉直状态.在绳的中点施加一个大小F=2.2N,方向垂直于绳沿水平向左的恒力,在F作用下两小球开始运动,以后两小球经过若干次碰撞,由于两小球之间有粘性,每一次碰撞后,小球垂直于F方向的速度将减小0.55m/s,当力F作用了2s时,两小球发生了最后一次碰撞,且不再分离.g取10m/s.求:(1)最后一次碰撞后,小球的加速度;
(2)最后一次碰撞结束时,小球的速度;
(3)整个碰撞过程中,系统损失的机械能;
(4)两小球相碰的总次数.
分析:(1)将两个小球看成整体,根据牛顿第二定律求加速度a.
(2)最后一次碰撞结束时,两小球粘合成一个整体,由运动学公式求解最后一次碰撞结束时小球的速度;
(3)整个碰撞过程中,F做功为F(
+
at2),转化为两小球的动能和内能,根据功能关系列式求解;
(4)根据功能关系求第一次碰撞前,两球在水平、竖直两个方向的分速度vx和vy.根据条件:每一次碰撞后,小球垂直于F方向的速度将减小0.55m/s,即可求出碰撞的次数.
(2)最后一次碰撞结束时,两小球粘合成一个整体,由运动学公式求解最后一次碰撞结束时小球的速度;
(3)整个碰撞过程中,F做功为F(
| L |
| 2 |
| 1 |
| 2 |
(4)根据功能关系求第一次碰撞前,两球在水平、竖直两个方向的分速度vx和vy.根据条件:每一次碰撞后,小球垂直于F方向的速度将减小0.55m/s,即可求出碰撞的次数.
解答:解:(1)最后一次碰撞结束时,两小球粘合成一个整体,根据牛顿第二定律得:F=2ma,则得a=5.5m/s.
(2)最后一次碰撞结束时,小球的速度为v=at=11m/s;
(3)整个碰撞过程中,系统损失的机械能为
△E=F(
+
at2)-
×2mv2
代入解得,△E=0.242J
(4)设第一次碰撞前,两球在水平、竖直两个方向的分速度分别为vx和vy.则根据功能关系得
F(
+S)=
×2m(
+
),
又由整体水平方向做匀加速运动,则有S=
解得,vy=1.1m/s
由题意,每一次碰撞后,小球垂直于F方向的速度将减小0.55m/s,则得:
两小球相碰的总次数n=
=2次
答:(1)最后一次碰撞后,小球的加速度为5.5m/s2;
(2)最后一次碰撞结束时,小球的速度为11m/s;
(3)整个碰撞过程中,系统损失的机械能为0.242J;
(4)两小球相碰的总次数为2次.
(2)最后一次碰撞结束时,小球的速度为v=at=11m/s;
(3)整个碰撞过程中,系统损失的机械能为
△E=F(
| L |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
代入解得,△E=0.242J
(4)设第一次碰撞前,两球在水平、竖直两个方向的分速度分别为vx和vy.则根据功能关系得
F(
| L |
| 2 |
| 1 |
| 2 |
| v | 2 x |
| v | 2 y |
又由整体水平方向做匀加速运动,则有S=
| ||
| 2a |
解得,vy=1.1m/s
由题意,每一次碰撞后,小球垂直于F方向的速度将减小0.55m/s,则得:
两小球相碰的总次数n=
| vy |
| 0.55 |
答:(1)最后一次碰撞后,小球的加速度为5.5m/s2;
(2)最后一次碰撞结束时,小球的速度为11m/s;
(3)整个碰撞过程中,系统损失的机械能为0.242J;
(4)两小球相碰的总次数为2次.
点评:本题关键采用整体法求水平方向的加速度,运用功能关系和运动学公式结合求碰前两个球的分速度.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 如图所示,两个质量均为m的小环套在一水平放置的粗糙长杆上,两根长度均为l的轻绳一端系在小环上,另一端系在质量为M的木块上,两个小环之间的距离也为l,小环保持静止.试求:
如图所示,两个质量均为m的小环套在一水平放置的粗糙长杆上,两根长度均为l的轻绳一端系在小环上,另一端系在质量为M的木块上,两个小环之间的距离也为l,小环保持静止.试求: (2011?保定模拟)如图所示,两个质量均为m的物体A和B,由轻绳和轻弹簧连接绕过不计摩擦力的定滑轮,系统静止,将另一质量也是m的物体C,轻放在A上,在刚放上A的瞬间( )
(2011?保定模拟)如图所示,两个质量均为m的物体A和B,由轻绳和轻弹簧连接绕过不计摩擦力的定滑轮,系统静止,将另一质量也是m的物体C,轻放在A上,在刚放上A的瞬间( )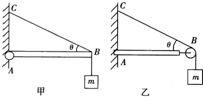 如图所示,两个质量均为m的物体分别挂在支架上的B点(如图甲所示)和跨过滑轮的轻绳BC上(如图乙所示),图甲中轻杆AB可绕A点转动,图乙中水平轻杆一端A插在墙壁内,已知θ=30°,则图甲中轻杆AB受到绳子的作用力F1和图乙中滑轮受到绳子的作用力F2分别为( )
如图所示,两个质量均为m的物体分别挂在支架上的B点(如图甲所示)和跨过滑轮的轻绳BC上(如图乙所示),图甲中轻杆AB可绕A点转动,图乙中水平轻杆一端A插在墙壁内,已知θ=30°,则图甲中轻杆AB受到绳子的作用力F1和图乙中滑轮受到绳子的作用力F2分别为( )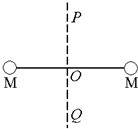 如图所示,两个质量均为M的星体,O为两星体连线中点,PQ是其连线的垂直平分线,一个质量为m的物体从O沿OP方向一直运动下去,则它受到的万有引力大小变化情况是( )
如图所示,两个质量均为M的星体,O为两星体连线中点,PQ是其连线的垂直平分线,一个质量为m的物体从O沿OP方向一直运动下去,则它受到的万有引力大小变化情况是( ) (2005?广州模拟)如图所示,两个质量均为4m的小球A和B由轻弹簧连接,置于光滑水平面上.一颗质量为m子弹,以水平速度v0射入A球,并在极短时间内嵌在其中.求:在运动过程中
(2005?广州模拟)如图所示,两个质量均为4m的小球A和B由轻弹簧连接,置于光滑水平面上.一颗质量为m子弹,以水平速度v0射入A球,并在极短时间内嵌在其中.求:在运动过程中