题目内容
16.在离地20m高处有一小球A做自由落体运动,A球由静止释放的同时,在其下方地面上另一个小球B以初速度v0竖直上抛,(不计空气阻力,g=10m/s2)(1)若要使两球在空中相遇,则B球上抛的初速度v0必须满足什么条件?
(2)若要使B球在上升阶段与A球相遇,则初速度v0必须满足什么条件?
(3)若要使B球在下落阶段与A球相遇,则初速度v0必须满足什么条件?
分析 A球做自由落体运动,B球做竖直上升运动,相遇时的最低点在落地点,求的B的最小速度速度,在上升过程中到达最高点相遇求的此时速度即可判断
解答 解:(1)A下落到地面的时间为$t=\sqrt{\frac{2h}{g}}=2s$
当AB刚好相遇时,B恰好落到地面,故B上升的时间为$t′=\frac{t}{2}=1s$,故B的最小速度为v0=gt′=10m/s,故v0≥10m/s
(2)A下降的高度为${h}_{1}=\frac{1}{2}g{t}^{2}$
B上升的高度为${h}_{2}={v}_{0}t-\frac{1}{2}g{t}^{2}$
相遇是H=h1+h2
当B上升到最高点时相遇则v0=gt
联立解得v0=$10\sqrt{2}m/s$
故速度${v}_{0}≥10\sqrt{2}m/s$
(3)在下降阶段相遇,结合(1)(2)可知,${10m/s≤v}_{0}≤10\sqrt{2}m/s$
答:(1)若要使两球在空中相遇,则B球上抛的初速度v0必须满足v0≥10m/s
(2)若要使B球在上升阶段与A球相遇,则初速度v0必须满足${v}_{0}≥10\sqrt{2}m/s$
(3)若要使B球在下落阶段与A球相遇,则初速度v0必须满足${10m/s≤v}_{0}≤10\sqrt{2}m/s$
点评 本题关键是明确竖直上抛运动和自由落体运动的运动性质,然后根据运动学公式列式求解,不难

练习册系列答案
相关题目
6.质量为M的人在游乐园乘坐过山车时,人随车在竖直平面内做圆周运动,下列说法中正确的是( )
| A. | 人在最高点时处于倒坐状态,如果没有保险带,人一定会掉下来 | |
| B. | 人在最低点时处于失重状态 | |
| C. | 人在最低点对座位的压力一定大于人的重力Mg | |
| D. | 人在最高点时对座位的压力一定小于人的重力Mg |
7.一辆汽车从拱形桥的顶端匀速率驶下,以下说法中正确的是( )
| A. | 它的动能变化量与重力势能的变化量大小相等 | |
| B. | 它的机械能守恒 | |
| C. | 所有力对汽车做功之和为零 | |
| D. | 重力对汽车做功与汽车重力势能变化量相等 |
7.物理定律多数是在大量实验的基础上归纳总结出来的.但也有些物理规律的建立并不是直接从实验得到的,而是经过了理想化(或合理)外推得到的.下列规律中属于理想化外推得到的是( )
| A. | 牛顿第一定律 | B. | 牛顿第二定律 | ||
| C. | 玻意耳定律 | D. | 法拉第电磁感应定律 |
5. 球A和球B可在光滑杆上无摩擦滑动,两球用一根细绳连接如图所示,球A的质量是球B的两倍,当杆以角速度ω匀速转动时,两球刚好保持与杆无相对滑动,那么( )
球A和球B可在光滑杆上无摩擦滑动,两球用一根细绳连接如图所示,球A的质量是球B的两倍,当杆以角速度ω匀速转动时,两球刚好保持与杆无相对滑动,那么( )
 球A和球B可在光滑杆上无摩擦滑动,两球用一根细绳连接如图所示,球A的质量是球B的两倍,当杆以角速度ω匀速转动时,两球刚好保持与杆无相对滑动,那么( )
球A和球B可在光滑杆上无摩擦滑动,两球用一根细绳连接如图所示,球A的质量是球B的两倍,当杆以角速度ω匀速转动时,两球刚好保持与杆无相对滑动,那么( )| A. | 球A受到的向心力大于B受到的向心力 | |
| B. | 球A转动的半径是球B转动半径的一半 | |
| C. | 当A球质量增大时,球A向外运动 | |
| D. | 当ω增大时,球B向外运动 |
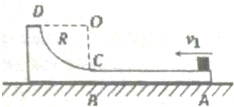 竖直平面内的轨道ABCD由水平滑道AB与半径为R的光滑的四分之一滑道CD组成,AB恰好与圆弧CD在C点相切,轨道放在光滑的水平面上,如图所示,一个质量为m=1kg的小物块(可视为质点)从轨道的A端以初速度v1=4m/s冲上水平滑道AB,沿着滑道运动,由DC弧滑下后最终停止在水平滑道AB的中间位置.已知水平滑道AB长为L=1m,轨道ABCD的质量为M=3kg.重力加速度g=10m/s2.求:
竖直平面内的轨道ABCD由水平滑道AB与半径为R的光滑的四分之一滑道CD组成,AB恰好与圆弧CD在C点相切,轨道放在光滑的水平面上,如图所示,一个质量为m=1kg的小物块(可视为质点)从轨道的A端以初速度v1=4m/s冲上水平滑道AB,沿着滑道运动,由DC弧滑下后最终停止在水平滑道AB的中间位置.已知水平滑道AB长为L=1m,轨道ABCD的质量为M=3kg.重力加速度g=10m/s2.求: 如图所示,小物体A在竖直平面内做匀速圆周运动,则小球A所受重力及杆对它的弹力F的受力示意图可能是(A、B选项中F方向与OA平行)( )
如图所示,小物体A在竖直平面内做匀速圆周运动,则小球A所受重力及杆对它的弹力F的受力示意图可能是(A、B选项中F方向与OA平行)( )



 应用如图所示的实验器材来研究电磁感应现象及判定感应电流方向.
应用如图所示的实验器材来研究电磁感应现象及判定感应电流方向.