题目内容
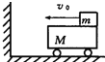
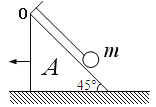
【题目】如图所示，质量为mc=4kg、长度为l=8m且两端带有弹性挡板的长木板C静止在水平地面上，D、E为长木板左右端点，P为中点，质量为mB=3.8kg的物块B静止在P点，一质量为mA=0.2kg的子弹A以v0=160m/s的速度水平飞来与B发生正碰并留在其中。重力加速度大小为g=10m/s2。求
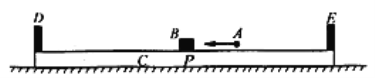
(1)当A、B与长木板C之间的动摩擦因数μ1=0.5时，B与C均向左运动，若B刚好与挡板没有发生碰撞，则C与地面之间的动摩擦因数μ2为多少?
(2)如果地面光滑，A、B与长木板C之间的动摩擦因数μ1′=0.08，且A、B整体与挡板发生弹性碰撞时刚好速度交换，则
I.B最终停在长木板上何处?
Ⅱ.从B开始运动到与长木板相对静止，B物块运动的总路程为多少?
【答案】(1)
(2)停在D端，22m
【解析】
A与B碰撞动量守恒，解得A与B碰撞后共同速度，由牛顿第二定律将AB当作整体加速度大小和木块C加速度大小，由运动学公式求出C与地面之间的动摩擦因数；A、B与长木板C滑动到共同速度，由动量守恒求出共同速度，由能量守恒求出A、B在长木板上滑动的相对路程，判断B最终停在长木板上何处；因为A、B与C碰撞时速度交换，在同一坐标系可得A、B和长木板C的速度-时间图像，求出从B开始运动到与长木板相对静止，B物块运动的总路程；
解：(1)设A与B碰撞后共同速度为
，碰撞后加速度为
，长木板C的加速度为
A与B碰撞动量守恒：
解得
将AB当作整体由牛顿第二定律有：
对木块C受力分析可得：
设经过时间t刚好不碰撞，由运动学公式有：
联立解得
(2) I、A、B与长木板C滑动到共同速度，由动量守恒可得：
解得：
令A、B在长木板上滑动的相对路程为
，则由能量守恒可得：
解得：
因为
，即B刚好停在D端
II、A、B的加速度为
长木板的加速度为
因为A、B与C碰撞时速度交换，在同一坐标系可得A、B和长木板C的速度-时间图像如（实线为A、B，虚线为长木板）
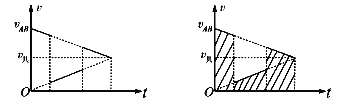
由图像可得B运动的总路程为
