题目内容
4.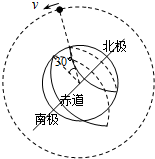 极地卫星的运行轨道平面通过地球的南北两极(轨道可视为圆轨道).如图所示,若某极地卫星从北纬30°的正上方按图示方向第一次运行至南纬60°正上方,所用时间为t,已知地球半径为R(地球可看做球体),地球表面的重力加速度为g,卫星距地面的高度为R,下列关系正确的是( )
极地卫星的运行轨道平面通过地球的南北两极(轨道可视为圆轨道).如图所示,若某极地卫星从北纬30°的正上方按图示方向第一次运行至南纬60°正上方,所用时间为t,已知地球半径为R(地球可看做球体),地球表面的重力加速度为g,卫星距地面的高度为R,下列关系正确的是( )| A. | t=π$\sqrt{\frac{R}{g}}$ | B. | t=$\frac{π}{2}$$\sqrt{\frac{R}{g}}$ | C. | t=π$\sqrt{\frac{2R}{g}}$ | D. | t=2π$\sqrt{\frac{2R}{g}}$ |
分析 根据地球表面重力等于万有引力,卫星运动的向心力由地球对卫星的万有引力提供列出等式求出极地卫星周期,再进行求解.
解答 解:根据地球表面的重力和万有引力相等
$\frac{GMm}{{R}^{2}}$=mg
卫星运动的向心力由地球对卫星的万有引力提供,
$\frac{GMm}{{r}^{2}}$=m$\frac{{4π}^{2}}{{T}^{2}}$r,r=2R
解得:T=4π$\sqrt{\frac{2R}{{g}^{\;}}}$,
从北纬30°的正上方按图示方向第一次运行至南纬60°正上方转过的圆心角为θ=$\frac{π}{2}$,
所以t=$\frac{T}{4}$=π$\sqrt{\frac{2R}{g}}$,
故选:C.
点评 灵活运动用重力和万有引力相等以及万有引力提供圆周运动的向心力是解决本题的关键.

练习册系列答案
相关题目
14.关于运动的合成与分解有以下说法,其中不正确的是( )
| A. | 两个直线运动的合位移一定比分位移大 | |
| B. | 运动的合成与分解都遵循平行四边形定则 | |
| C. | 两个分运动总是同时进行着的 | |
| D. | 某个分运动的规律不会因另一个分运动而改变 |
15.印刷厂里为使纸张好用,主要应控制厂房内的( )
| A. | 绝对湿度 | B. | 相对湿度 | C. | 温度 | D. | 大气压强 |
12.小球做匀速圆周运动的过程,以下各物理量不发生变化的是( )
| A. | 线速度 | B. | 合外力 | C. | 周期 | D. | 向心加速度 |
19.一辆汽车从车站从静止做匀加速直线运动,开出一段时间之后,司机发现一乘客未上车,便紧急刹车做匀减速运动.从启运到停止一共经历t=20s,前进了30m,在此过程中,汽车的最大速度为( )
| A. | 1.5m/s | B. | 4m/s | C. | 3m/s | D. | 无法确定 |
9. 如图所示,甲和乙为电流最大值相等的方波交流电流和正弦交流电流图象,则这两个电热器的电功率之比P甲:P乙为( )
如图所示,甲和乙为电流最大值相等的方波交流电流和正弦交流电流图象,则这两个电热器的电功率之比P甲:P乙为( )
 如图所示,甲和乙为电流最大值相等的方波交流电流和正弦交流电流图象,则这两个电热器的电功率之比P甲:P乙为( )
如图所示,甲和乙为电流最大值相等的方波交流电流和正弦交流电流图象,则这两个电热器的电功率之比P甲:P乙为( )| A. | 1:1 | B. | 1:2 | C. | 2:1 | D. | $\sqrt{2}$:1 |
16.下列哪些因素会使“研究平抛运动”实验的误差减小( )
| A. | 每次释放小球的位置必须不同 | |
| B. | 安装斜槽时其末端不水平 | |
| C. | 建立坐标系时,以斜槽末端端口位置为坐标原点 | |
| D. | 根据曲线计算平抛运动的初速度时,在曲线上取作计算的点离原点O较远 | |
| E. | 固定白纸的木板必须调节成竖直 |
13. 图中K、L、M为静电场中的三个相距很近的等势面(K、M之间无电荷).一带电粒子射入此静电场中后,仅受电场力作用,沿a→b→c→d→e路径运动.已知电势φK<φL<φM.下列说法中正确的是( )
图中K、L、M为静电场中的三个相距很近的等势面(K、M之间无电荷).一带电粒子射入此静电场中后,仅受电场力作用,沿a→b→c→d→e路径运动.已知电势φK<φL<φM.下列说法中正确的是( )
 图中K、L、M为静电场中的三个相距很近的等势面(K、M之间无电荷).一带电粒子射入此静电场中后,仅受电场力作用,沿a→b→c→d→e路径运动.已知电势φK<φL<φM.下列说法中正确的是( )
图中K、L、M为静电场中的三个相距很近的等势面(K、M之间无电荷).一带电粒子射入此静电场中后,仅受电场力作用,沿a→b→c→d→e路径运动.已知电势φK<φL<φM.下列说法中正确的是( )| A. | 粒子带负电 | B. | 粒子在bc段做加速运动 | ||
| C. | 粒子在b点与d点的速率大小相等 | D. | 粒子在C点时电势能最小 |
14.一束光从空气中射向折射率为$\sqrt{3}$的玻璃表面,如图所示,θ1代表入射角,则( )


| A. | θ1>60°时会发生全反射现象 | |
| B. | 无论入射角θ1多大,折射角θ2都不会大于45° | |
| C. | 入射角θ1=arctan$\sqrt{3}$时,反射光线跟折射光线恰好垂直 | |
| D. | 只有当光从玻璃射向空气和玻璃的交界面时才可能发生全反射 |