题目内容
9. 如图所示,甲和乙为电流最大值相等的方波交流电流和正弦交流电流图象,则这两个电热器的电功率之比P甲:P乙为( )
如图所示,甲和乙为电流最大值相等的方波交流电流和正弦交流电流图象,则这两个电热器的电功率之比P甲:P乙为( )| A. | 1:1 | B. | 1:2 | C. | 2:1 | D. | $\sqrt{2}$:1 |
分析 方波的电流有效值Ia=Im,正弦交流电的有效值Ib=$\frac{\sqrt{2}}{2}$Im.根据功率公式P=I2R,由电流的有效值求解功率,再算出比值.
解答 解:方波的电流有效值Ia=Im,正弦交流电的有效值Ib=$\frac{\sqrt{2}}{2}$Im
根据功率公式P=I2R得到
Pa:Pb=Ia2:Ib2=Im2:($\frac{\sqrt{2}}{2}$Im)2=2:1
故选:C.
点评 对于交变电流求解热量、热功率、电功等都应用有效值,求解电量用平均值.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
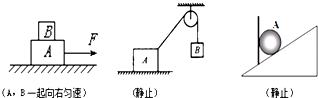
17. 在探究摩擦力变化规律的实验中,特设计了如甲图所示的演示装置,力传感器A与计算机连接,可获得力随时间变化的规律,将力传感器固定在光滑水平桌面上,测力端通过细绳与一滑块相连(调节传感器高度可使细绳水平),滑块放在较长的小车上,小车一端连接一根轻绳并跨过光滑的轻定滑轮系一只空沙桶(调节滑轮可使桌面上部细绳水平),整个装置处于静止状态.实验开始时打开传感器同时缓慢向沙桶里倒入沙子,小车一旦运动起来,立即停止倒沙子,若力传感器采集的图象如乙图所示,则结合该图象,下列说法中正确的是( )
在探究摩擦力变化规律的实验中,特设计了如甲图所示的演示装置,力传感器A与计算机连接,可获得力随时间变化的规律,将力传感器固定在光滑水平桌面上,测力端通过细绳与一滑块相连(调节传感器高度可使细绳水平),滑块放在较长的小车上,小车一端连接一根轻绳并跨过光滑的轻定滑轮系一只空沙桶(调节滑轮可使桌面上部细绳水平),整个装置处于静止状态.实验开始时打开传感器同时缓慢向沙桶里倒入沙子,小车一旦运动起来,立即停止倒沙子,若力传感器采集的图象如乙图所示,则结合该图象,下列说法中正确的是( )
 在探究摩擦力变化规律的实验中,特设计了如甲图所示的演示装置,力传感器A与计算机连接,可获得力随时间变化的规律,将力传感器固定在光滑水平桌面上,测力端通过细绳与一滑块相连(调节传感器高度可使细绳水平),滑块放在较长的小车上,小车一端连接一根轻绳并跨过光滑的轻定滑轮系一只空沙桶(调节滑轮可使桌面上部细绳水平),整个装置处于静止状态.实验开始时打开传感器同时缓慢向沙桶里倒入沙子,小车一旦运动起来,立即停止倒沙子,若力传感器采集的图象如乙图所示,则结合该图象,下列说法中正确的是( )
在探究摩擦力变化规律的实验中,特设计了如甲图所示的演示装置,力传感器A与计算机连接,可获得力随时间变化的规律,将力传感器固定在光滑水平桌面上,测力端通过细绳与一滑块相连(调节传感器高度可使细绳水平),滑块放在较长的小车上,小车一端连接一根轻绳并跨过光滑的轻定滑轮系一只空沙桶(调节滑轮可使桌面上部细绳水平),整个装置处于静止状态.实验开始时打开传感器同时缓慢向沙桶里倒入沙子,小车一旦运动起来,立即停止倒沙子,若力传感器采集的图象如乙图所示,则结合该图象,下列说法中正确的是( )| A. | 可求出空沙桶的重力 | |
| B. | 可求出滑块与小车之间的滑动摩擦力的大小 | |
| C. | 可求出滑块与小车之间的最大静摩擦力的大小 | |
| D. | 可判断第5秒后小车做匀速直线运动(滑块仍在车上) |
4. 极地卫星的运行轨道平面通过地球的南北两极(轨道可视为圆轨道).如图所示,若某极地卫星从北纬30°的正上方按图示方向第一次运行至南纬60°正上方,所用时间为t,已知地球半径为R(地球可看做球体),地球表面的重力加速度为g,卫星距地面的高度为R,下列关系正确的是( )
极地卫星的运行轨道平面通过地球的南北两极(轨道可视为圆轨道).如图所示,若某极地卫星从北纬30°的正上方按图示方向第一次运行至南纬60°正上方,所用时间为t,已知地球半径为R(地球可看做球体),地球表面的重力加速度为g,卫星距地面的高度为R,下列关系正确的是( )
 极地卫星的运行轨道平面通过地球的南北两极(轨道可视为圆轨道).如图所示,若某极地卫星从北纬30°的正上方按图示方向第一次运行至南纬60°正上方,所用时间为t,已知地球半径为R(地球可看做球体),地球表面的重力加速度为g,卫星距地面的高度为R,下列关系正确的是( )
极地卫星的运行轨道平面通过地球的南北两极(轨道可视为圆轨道).如图所示,若某极地卫星从北纬30°的正上方按图示方向第一次运行至南纬60°正上方,所用时间为t,已知地球半径为R(地球可看做球体),地球表面的重力加速度为g,卫星距地面的高度为R,下列关系正确的是( )| A. | t=π$\sqrt{\frac{R}{g}}$ | B. | t=$\frac{π}{2}$$\sqrt{\frac{R}{g}}$ | C. | t=π$\sqrt{\frac{2R}{g}}$ | D. | t=2π$\sqrt{\frac{2R}{g}}$ |
1.在交通事故分析中,刹车线的长度是很重要的依据,刹车线是汽车刹车后,停止转动的轮胎在地面上滑动时留下的痕迹.在某次交通事故中,汽车刹车线的长度是14m,假设汽车刹车时的速度大小为14m/s,则汽车刹车时的加速度大小为( )
| A. | 7m/s2 | B. | 17m/s2 | C. | 14m/s2 | D. | 3.5m/s2 |
18. 如图所示,两根质量同为m、电阻同为R、长度同为l的导体棒a、b,用两条等长的、质量和电阻均可忽略不计的长直导线连接后,放在距地面足够高的光滑绝缘水平桌面上,两根导体棒均与桌边缘平行,一根在桌面上,另一根移动到靠在桌子的光滑绝缘侧面上.整个空间存在水平向右的匀强磁场,磁感应强度为B,开始时两棒静止,自由释放后开始运动.已知两条导线除桌边缘拐弯处外其余部位均处于伸直状态,导线与桌子侧棱间无摩擦.( )
如图所示,两根质量同为m、电阻同为R、长度同为l的导体棒a、b,用两条等长的、质量和电阻均可忽略不计的长直导线连接后,放在距地面足够高的光滑绝缘水平桌面上,两根导体棒均与桌边缘平行,一根在桌面上,另一根移动到靠在桌子的光滑绝缘侧面上.整个空间存在水平向右的匀强磁场,磁感应强度为B,开始时两棒静止,自由释放后开始运动.已知两条导线除桌边缘拐弯处外其余部位均处于伸直状态,导线与桌子侧棱间无摩擦.( )
 如图所示,两根质量同为m、电阻同为R、长度同为l的导体棒a、b,用两条等长的、质量和电阻均可忽略不计的长直导线连接后,放在距地面足够高的光滑绝缘水平桌面上,两根导体棒均与桌边缘平行,一根在桌面上,另一根移动到靠在桌子的光滑绝缘侧面上.整个空间存在水平向右的匀强磁场,磁感应强度为B,开始时两棒静止,自由释放后开始运动.已知两条导线除桌边缘拐弯处外其余部位均处于伸直状态,导线与桌子侧棱间无摩擦.( )
如图所示,两根质量同为m、电阻同为R、长度同为l的导体棒a、b,用两条等长的、质量和电阻均可忽略不计的长直导线连接后,放在距地面足够高的光滑绝缘水平桌面上,两根导体棒均与桌边缘平行,一根在桌面上,另一根移动到靠在桌子的光滑绝缘侧面上.整个空间存在水平向右的匀强磁场,磁感应强度为B,开始时两棒静止,自由释放后开始运动.已知两条导线除桌边缘拐弯处外其余部位均处于伸直状态,导线与桌子侧棱间无摩擦.( )| A. | 刚释放时,导体棒a、b的加速度大小都为g | |
| B. | 导体棒a、b运动稳定时的速度大小$\frac{2mgR}{{B}^{2}{l}^{2}}$ | |
| C. | 若从开始下滑到刚稳定时通过横截面的电荷量为q,该过程中系统产生的焦耳热$\frac{2mgqR}{Bl}$-$\frac{4{m}^{3}{g}^{2}{R}^{2}}{{B}^{4}{l}^{4}}$ | |
| D. | 若绝缘水平面不光滑,导体棒a、b运动稳定时导线上拉力为零 |
19.关于电源电动势E的下列说法中正确的是( )
| A. | 电动势在数值上等于电源将单位正电荷从负极移动到正极时,非静电力所做的功 | |
| B. | 由电动势E=$\frac{{W}_{非}}{q}$可知,电源内非静电力做功越多,电动势越大 | |
| C. | 电动势E的单位与电势差的单位相同,都是伏特,所以电势差就是电动势 | |
| D. | 电源的电动势与外电路结构有关,外电路变化,通常电动势也要变化 |

 在“用油膜法估测分子的大小”的实验中,所用油酸酒精溶液的浓度为每104 mL溶液中有纯油酸6mL,用注射器测得1mL上述溶液为75滴.把1滴该溶液滴入盛水的浅盘里,待水面稳定后,将玻璃板放在浅盘上,用彩笔在玻璃板上描出油膜的轮廊,再把玻璃板放在坐标纸上,其形状和尺寸如图所示,坐标中正方形方格的边长为1cm.则
在“用油膜法估测分子的大小”的实验中,所用油酸酒精溶液的浓度为每104 mL溶液中有纯油酸6mL,用注射器测得1mL上述溶液为75滴.把1滴该溶液滴入盛水的浅盘里,待水面稳定后,将玻璃板放在浅盘上,用彩笔在玻璃板上描出油膜的轮廊,再把玻璃板放在坐标纸上,其形状和尺寸如图所示,坐标中正方形方格的边长为1cm.则