题目内容
11.轻质弹簧的劲度系数为k,弹簧上的弹力与其形变量成正比,把轻弹簧的一端固定,另一端连接用未知大小的力缓解压缩弹簧,从弹簧的自然长度压缩到形变量为x,如图所示,求被压缩长度为x时,弹簧储存的弹性势能.
分析 根据胡克定律找到力与位移关系,F-l图象为过原点的斜直线,图象的面积表示力做功,然后结合功能关系即可求出.
解答  解:根据F=kl知F-l图象为过原点的斜直线,如图图象的面积表示力做功为:
解:根据F=kl知F-l图象为过原点的斜直线,如图图象的面积表示力做功为:
W=$\frac{0+kl}{2}•l$=$\frac{1}{2}k{l}^{2}$
该过程中,外力对弹簧做的功转化为弹簧的弹性势能,所以储存的弹性势能是$\frac{1}{2}k{l}^{2}$.
答:储存的弹性势能是$\frac{1}{2}k{l}^{2}$.
点评 此题结合功能关系,考查胡克定律和F-l图象的面积表示力做功的大小,理解功的物理量意义是力在空间中的积累效果即可正确解答.基础题目.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
1.放射性元素${\;}_{b}^{a}$X的衰变反应是:${\;}_{b}^{a}$X→${\;}_{d}^{c}$Y+N,其中N是未知的射线,则下列说法正确的是( )
| A. | 若此衰变为β衰变,则b=d+1 | |
| B. | 若此衰变为α衰变,则a=c+4 | |
| C. | 若放射性元素${\;}_{b}^{a}$X经过6 h还剩下$\frac{1}{8}$没有衰变,则它的半衰期为2 h | |
| D. | 用射线N照射锌板一定可使锌板带电 |
2.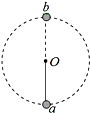 如图所示,细杆的一端与小球相连,可绕过O点的水平轴自由转动,细杆长0.5m,小球质量为3.0kg.现给小球一初速度使它做圆周运动,若小球通过轨道最低点a处的速度为va=6m/s,通过轨道最高点b处的速度为vb=2m/s,取g=10m/s2,则小球通过最低点和最高点时对细杆作用力的情况是( )
如图所示,细杆的一端与小球相连,可绕过O点的水平轴自由转动,细杆长0.5m,小球质量为3.0kg.现给小球一初速度使它做圆周运动,若小球通过轨道最低点a处的速度为va=6m/s,通过轨道最高点b处的速度为vb=2m/s,取g=10m/s2,则小球通过最低点和最高点时对细杆作用力的情况是( )
 如图所示,细杆的一端与小球相连,可绕过O点的水平轴自由转动,细杆长0.5m,小球质量为3.0kg.现给小球一初速度使它做圆周运动,若小球通过轨道最低点a处的速度为va=6m/s,通过轨道最高点b处的速度为vb=2m/s,取g=10m/s2,则小球通过最低点和最高点时对细杆作用力的情况是( )
如图所示,细杆的一端与小球相连,可绕过O点的水平轴自由转动,细杆长0.5m,小球质量为3.0kg.现给小球一初速度使它做圆周运动,若小球通过轨道最低点a处的速度为va=6m/s,通过轨道最高点b处的速度为vb=2m/s,取g=10m/s2,则小球通过最低点和最高点时对细杆作用力的情况是( )| A. | a处为拉力,方向竖直向下,大小为246N | |
| B. | a处为拉力,方向竖直向上,大小为246N | |
| C. | b处为拉力,方向竖直向下,大小为6N | |
| D. | b处为压力,方向竖直向下,大小为6N |
19.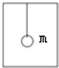 如图所示,升降机内质量为m的小球用轻绳系住,悬在升降机内,当升降机以a=$\frac{2}{3}$g减速上升时,悬绳的拉力为( )
如图所示,升降机内质量为m的小球用轻绳系住,悬在升降机内,当升降机以a=$\frac{2}{3}$g减速上升时,悬绳的拉力为( )
 如图所示,升降机内质量为m的小球用轻绳系住,悬在升降机内,当升降机以a=$\frac{2}{3}$g减速上升时,悬绳的拉力为( )
如图所示,升降机内质量为m的小球用轻绳系住,悬在升降机内,当升降机以a=$\frac{2}{3}$g减速上升时,悬绳的拉力为( )| A. | $\frac{2mg}{3}$ | B. | $\frac{mg}{3}$ | C. | $\frac{4mg}{3}$ | D. | mg |
6.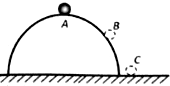 竖直平面内半径为R的光滑圆轨道外侧,一小球受到微小扰动从A点由静止开始沿圆轨道下滑,至B点时脱离轨道,最终落在水平面上的C点,不计空气阻力,下列说法正确的是( )
竖直平面内半径为R的光滑圆轨道外侧,一小球受到微小扰动从A点由静止开始沿圆轨道下滑,至B点时脱离轨道,最终落在水平面上的C点,不计空气阻力,下列说法正确的是( )
 竖直平面内半径为R的光滑圆轨道外侧,一小球受到微小扰动从A点由静止开始沿圆轨道下滑,至B点时脱离轨道,最终落在水平面上的C点,不计空气阻力,下列说法正确的是( )
竖直平面内半径为R的光滑圆轨道外侧,一小球受到微小扰动从A点由静止开始沿圆轨道下滑,至B点时脱离轨道,最终落在水平面上的C点,不计空气阻力,下列说法正确的是( )| A. | 在B点时,小球对圆轨道的压力为零 | |
| B. | B到C过程,小球做匀变速运动 | |
| C. | A到B过程,小球水平方向的加速度不断增大 | |
| D. | A到B过程,小球向心加速度不断增大 |
20.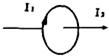 一根长直导线穿过载流金属环中心且垂直与金属环的平面,导线和环中的电流方向如图所示,那么金属环受的力( )
一根长直导线穿过载流金属环中心且垂直与金属环的平面,导线和环中的电流方向如图所示,那么金属环受的力( )
 一根长直导线穿过载流金属环中心且垂直与金属环的平面,导线和环中的电流方向如图所示,那么金属环受的力( )
一根长直导线穿过载流金属环中心且垂直与金属环的平面,导线和环中的电流方向如图所示,那么金属环受的力( )| A. | 等于零 | B. | 沿着环半径向外 | C. | 向左 | D. | 向右 |
 在做“研究平抛物体的运动”的实验中,为了确定小球在不同时刻在空中所通过的位置,实验时用了如图所示的装置.先将斜槽轨道的末端调整水平,在一块平整的木板表面钉上白纸和复写纸.将该木板竖直立于水平地面上,使一小球从斜槽上紧靠挡板处由静止释放,小球撞到木板并在白纸上留下痕迹A;将木板向远离槽口平移距离x,再使小球从斜槽上紧靠挡板处由静止释放,小球撞在木板上得到痕迹B;又将木板再向远离槽口平移距离x,小球再从斜槽上紧靠挡板处由静止释放,再得到痕迹C.若测得木板每次移动距离x=10.00cm,A、B间距离y1=5.02cm,B、C间距离y2=14.82cm.请回答以下问题(g=9.80m/s2)
在做“研究平抛物体的运动”的实验中,为了确定小球在不同时刻在空中所通过的位置,实验时用了如图所示的装置.先将斜槽轨道的末端调整水平,在一块平整的木板表面钉上白纸和复写纸.将该木板竖直立于水平地面上,使一小球从斜槽上紧靠挡板处由静止释放,小球撞到木板并在白纸上留下痕迹A;将木板向远离槽口平移距离x,再使小球从斜槽上紧靠挡板处由静止释放,小球撞在木板上得到痕迹B;又将木板再向远离槽口平移距离x,小球再从斜槽上紧靠挡板处由静止释放,再得到痕迹C.若测得木板每次移动距离x=10.00cm,A、B间距离y1=5.02cm,B、C间距离y2=14.82cm.请回答以下问题(g=9.80m/s2)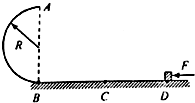 如图所示,半径为R的光滑半圆环轨道AB与一水平轨道BCD相切于B,AB轨道固定在竖直平面内,水平轨道的BC段光滑、CD段粗糙,在水平轨道上D点放置一可视为质点的小滑块,小滑块在大小为F的水平推力作用下运动.到B点时撤去推力F,小滑块恰能通过半圆环轨道最高点A,已知小滑块质量为m,B、C间距离sBC与C、D间距离sCD相等,且sBC=sCD=2R,求:
如图所示,半径为R的光滑半圆环轨道AB与一水平轨道BCD相切于B,AB轨道固定在竖直平面内,水平轨道的BC段光滑、CD段粗糙,在水平轨道上D点放置一可视为质点的小滑块,小滑块在大小为F的水平推力作用下运动.到B点时撤去推力F,小滑块恰能通过半圆环轨道最高点A,已知小滑块质量为m,B、C间距离sBC与C、D间距离sCD相等,且sBC=sCD=2R,求: 如图所示,一辆汽车走钢丝横跨尼罗河,如果汽车的总质量为2000kg,两侧的钢索弯曲成150°夹角,求每条钢索所受拉力的大小(钢索的质量可不计,cos75°=0.259,g=10N/kg).
如图所示,一辆汽车走钢丝横跨尼罗河,如果汽车的总质量为2000kg,两侧的钢索弯曲成150°夹角,求每条钢索所受拉力的大小(钢索的质量可不计,cos75°=0.259,g=10N/kg).