题目内容
3.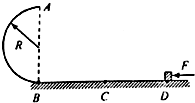 如图所示,半径为R的光滑半圆环轨道AB与一水平轨道BCD相切于B,AB轨道固定在竖直平面内,水平轨道的BC段光滑、CD段粗糙,在水平轨道上D点放置一可视为质点的小滑块,小滑块在大小为F的水平推力作用下运动.到B点时撤去推力F,小滑块恰能通过半圆环轨道最高点A,已知小滑块质量为m,B、C间距离sBC与C、D间距离sCD相等,且sBC=sCD=2R,求:
如图所示,半径为R的光滑半圆环轨道AB与一水平轨道BCD相切于B,AB轨道固定在竖直平面内,水平轨道的BC段光滑、CD段粗糙,在水平轨道上D点放置一可视为质点的小滑块,小滑块在大小为F的水平推力作用下运动.到B点时撤去推力F,小滑块恰能通过半圆环轨道最高点A,已知小滑块质量为m,B、C间距离sBC与C、D间距离sCD相等,且sBC=sCD=2R,求:(1)小滑块运动到B点时的速度大小;
(2)小滑块与CD间的动縻擦因数μ.
分析 (1)由小球恰好通过最高点,利用牛顿第二定律可求得最高点的速度;再对AB过程分析,由机械能守恒定律可求得B点的速度;
(2)对DB过程由动能定理列式可求得动摩擦因数的大小.
解答 解:(1)由于小滑块恰好通过A,设其速度为vA,由牛顿第二定律有:
mg=m$\frac{{{v}^{2}}_{A}}{R}$
小滑块从最低点B到最高点A的过程中,设最低点速度为vB,由机械能守恒定律有:
$\frac{1}{2}$mvB2=$\frac{1}{2}$mA2+mg2R
联立解得:vB=$\sqrt{5gR}$
(2)小滑块从D点运动到B点的过程中,推力F做功为W1,克服摩擦力做功为W2,则
W1=4FR
W2=2μmgR
由动能定理有:
W1-W2=$\frac{1}{2}$mvB2
联立解得:μ=$\frac{2F}{mg}$-1.25
答:(1)小滑块运动到B点时的速度大小为$\sqrt{5gR}$;
(2)小滑块与CD间的动縻擦因数μ为$\frac{2F}{mg}$-1.25
点评 本题考查动能定理、机械能守恒与圆周运动的综合应用,要注意小球恰好通过最高点的条件为重力充当向心力;再对过程分析,应用动能定理即可求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.下列说法正确的是( )
| A. | 开普勒发现了万有引力定律,卡文迪许测量了万有引力常量 | |
| B. | 从万有引力定律的表达式可知,当r趋近于零时,两物体间的万有引力无穷大 | |
| C. | 地球上物体随地球自转的向心加速度方向都指向地心,且赤道上物体的向心加速度比两扱处大 | |
| D. | 地球的第一宇宙速度为7.9km/s,它是人造地球卫星的最小发射速度.也是最大环绕速度 |
12.关于自由落体运动,下列说怯中正确的是( )
| A. | 某段位移内的平均速度等于初速度与末速度和的一半 | |
| B. | 某段时间内的平均速度等于初速度与末速度和的一半 | |
| C. | 在任何相等的时间内速度的变化量相等 | |
| D. | 在任何相等的时间内位移的增量相等 |
17.以初速度v=20m/s竖直向上抛一个小球(g=10m/s2),以下说法正确的是( )
| A. | 小球经过4s达到最高点 | |
| B. | 小球上升的最大高度为20m | |
| C. | 小球在出发点上方15m时,速度大小为10m/s | |
| D. | 小球到出发点上方15m时,经过了时间一定是1s |


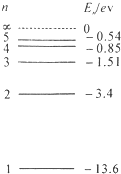 氢原子的能级如图所示,已知可见光的光子能量在1.62ev-3.11ev之间.下列说法正确的是ACD.(填正确答案标号.选对一个得3分,选对2个得4分,选对3个得6分.每选错1个扣3分,最低得分为0分)
氢原子的能级如图所示,已知可见光的光子能量在1.62ev-3.11ev之间.下列说法正确的是ACD.(填正确答案标号.选对一个得3分,选对2个得4分,选对3个得6分.每选错1个扣3分,最低得分为0分)