15.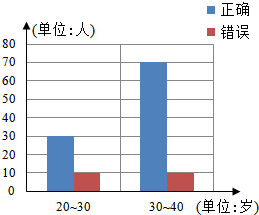 “开门大吉”是某电视台推出的游戏益智节目.选手面对1-4号4扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.正确回答每一扇门后,选手可自由选择带着奖金离开比赛,还可继续挑战后面的门以获得更多奖金(奖金金额累加),但是一旦回答错误,奖金将清零,选手也会离开比赛.在一次场外调查中,发现参加比赛的选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否人数如图所示.
“开门大吉”是某电视台推出的游戏益智节目.选手面对1-4号4扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.正确回答每一扇门后,选手可自由选择带着奖金离开比赛,还可继续挑战后面的门以获得更多奖金(奖金金额累加),但是一旦回答错误,奖金将清零,选手也会离开比赛.在一次场外调查中,发现参加比赛的选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否人数如图所示.
(1)写出2×2列联表;判断是否有90%的把握认为猜对歌曲名称与否与年龄有关?说明你的理由.(下面的临界值表供参考)
(参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
(理)(2)若某选手能正确回答第一、二、三、四扇门的概率分别为$\frac{4}{5}$,$\frac{3}{4}$,$\frac{2}{3}$,$\frac{1}{3}$,正确回答一个问题后,选择继续回答下一个问题的概率是$\frac{1}{2}$,且各个问题回答正确与否互不影响.设该选手所获梦想基金总数为ξ,求ξ的分布列及数学期望.
每扇门对应的梦想基金:(单位:元)
(文)(2)现计划在这次场外调查中按年龄段用分层抽样的方法选取6名选手,并抽取3名幸运选手,求3名幸运选手中至少有一人在20~30岁之间的概率.
 “开门大吉”是某电视台推出的游戏益智节目.选手面对1-4号4扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.正确回答每一扇门后,选手可自由选择带着奖金离开比赛,还可继续挑战后面的门以获得更多奖金(奖金金额累加),但是一旦回答错误,奖金将清零,选手也会离开比赛.在一次场外调查中,发现参加比赛的选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否人数如图所示.
“开门大吉”是某电视台推出的游戏益智节目.选手面对1-4号4扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.正确回答每一扇门后,选手可自由选择带着奖金离开比赛,还可继续挑战后面的门以获得更多奖金(奖金金额累加),但是一旦回答错误,奖金将清零,选手也会离开比赛.在一次场外调查中,发现参加比赛的选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否人数如图所示.(1)写出2×2列联表;判断是否有90%的把握认为猜对歌曲名称与否与年龄有关?说明你的理由.(下面的临界值表供参考)
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(理)(2)若某选手能正确回答第一、二、三、四扇门的概率分别为$\frac{4}{5}$,$\frac{3}{4}$,$\frac{2}{3}$,$\frac{1}{3}$,正确回答一个问题后,选择继续回答下一个问题的概率是$\frac{1}{2}$,且各个问题回答正确与否互不影响.设该选手所获梦想基金总数为ξ,求ξ的分布列及数学期望.
| 第一扇门 | 第二扇门 | 第三扇门 | 第四扇门 |
| 1000 | 2000 | 3000 | 5000 |
(文)(2)现计划在这次场外调查中按年龄段用分层抽样的方法选取6名选手,并抽取3名幸运选手,求3名幸运选手中至少有一人在20~30岁之间的概率.
12.(理)现有11个保送大学的名额分配给8个班级,每班至少有1个名额,则名额分配的方法共有( )
| A. | 56种 | B. | 112种 | C. | 120种 | D. | 240种 |
11.已知集合A={x|x2-x-6<0},$B=\{x\left|{y=\sqrt{x-m}}\right.\}$.若A∩B≠∅,则实数m的取值范围是( )
0 252531 252539 252545 252549 252555 252557 252561 252567 252569 252575 252581 252585 252587 252591 252597 252599 252605 252609 252611 252615 252617 252621 252623 252625 252626 252627 252629 252630 252631 252633 252635 252639 252641 252645 252647 252651 252657 252659 252665 252669 252671 252675 252681 252687 252689 252695 252699 252701 252707 252711 252717 252725 266669
| A. | (-∞,3) | B. | (-2,3) | C. | (-∞,-2) | D. | [3,+∞) |
 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,A为短轴的一个端点,且|OA|=|OF|,△AOF的面积为1(其中O为坐标原点).
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,A为短轴的一个端点,且|OA|=|OF|,△AOF的面积为1(其中O为坐标原点).