题目内容
14.已知定义在R上的函数f(x)、g(x)满足$\frac{f(x)}{g(x)}={a^x}$,且f′(x)g(x)>f(x)g′(x),$\frac{f(1)}{g(1)}+\frac{f(-1)}{g(-1)}=\frac{10}{3}$,若cn=$\frac{f(n)}{g(n)}$,则数列{ncn}的前n项和Sn=$\frac{3+(2n-1)•{3}^{n+1}}{4}$.分析 根据$\frac{f(x)}{g(x)}={a^x}$,结合题中等式建立关于a的方程:a+$\frac{1}{a}$=$\frac{10}{3}$,解之得a=3或$\frac{1}{3}$.再根据f′(x)g(x)>f(x)g′(x)可证出y=ax是R上的增函数,得a>1,由此可得a=3,求得ncn=n•3n,再由数列的求和方法:错位相减法,结合等比数列的求和公式,化简整理即可得到.
解答 解:∵$\frac{f(x)}{g(x)}={a^x}$,∴$\frac{f(1)}{g(1)}$=a,$\frac{f(-1)}{g(-1)}$=$\frac{1}{a}$,
因此$\frac{f(1)}{g(1)}+\frac{f(-1)}{g(-1)}=\frac{10}{3}$,即a+$\frac{1}{a}$=$\frac{10}{3}$.
解之得a=3或$\frac{1}{3}$.
设F(x)=$\frac{f(x)}{g(x)}$,则F'(x)=$\frac{f′(x)g(x)-f(x)g′(x)}{{g}^{2}(x)}$,
∵f'(x)g(x)>f(x)g'(x),
∴F'(x)>0在R上成立,故F(x)是R上的增函数.
即y=ax是R上的增函数,故a>1.则有a=3.
cn=$\frac{f(n)}{g(n)}$=3n,ncn=n•3n,
则前n项和Sn=1•3+2•32+3•33+…+n•3n,
3Sn=1•32+2•33+3•34+…+n•3n+1,
两式相减可得,-2Sn=3+32+33+…+3n-n•3n+1
=$\frac{3(1-{3}^{n})}{1-3}$-n•3n+1,
化简可得Sn=$\frac{3+(2n-1)•{3}^{n+1}}{4}$.
故答案为:$\frac{3+(2n-1)•{3}^{n+1}}{4}$.
点评 本题考查指数函数的单调性的运用,以及导数的运算法则的逆用,同时考查数列的求和方法:错位相减法,属于中档题.

 计算高手系列答案
计算高手系列答案| A. | 向左平行移动$\frac{π}{3}$个单位长度 | B. | 向右平行移动$\frac{π}{3}$个单位长度 | ||
| C. | 向左平行移动$\frac{π}{6}$个单位长度 | D. | 向右平行移动$\frac{π}{6}$个单位长度 |
| A. | “?x∈R,x2≥x”的否定为“?x∉R,x2≥x” | |
| B. | 命题“若x=1,则x2=1”逆命题 | |
| C. | “若$\sqrt{3}x(x≠0)$是有理数,则x为无理数”的逆否命题 | |
| D. | “x<-1”是“x2-1>0”的必要不充分条件条件 |
| A. | 0 | B. | $\frac{25}{2}$ | C. | 25 | D. | 50 |
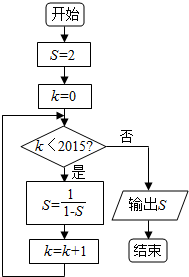
| A. | 2015 | B. | -1 | C. | $\frac{1}{2}$ | D. | 2 |
| A. | 命题“若x>1,则x2>1”的否命题 | |
| B. | 命题“若x>y,则|x|>y”的逆命题 | |
| C. | 若k<5,则两椭圆$\frac{x^2}{9}+\frac{y^2}{5}=1$与$\frac{x^2}{9-k}+\frac{y^2}{5-k}=1$有不同的焦点 | |
| D. | 命题“若方程x2+ky2=2表示焦点在y轴上的椭圆,则k的取值范围为(0,1)”的逆否命题 |
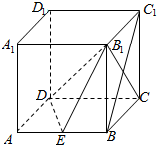 如图,在正方体ABCD-A1B1C1D1的棱长为a,E为棱AB上的一动点.
如图,在正方体ABCD-A1B1C1D1的棱长为a,E为棱AB上的一动点.