14.若椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的面积为abπ,则${∫}_{0}^{\frac{\sqrt{2}}{2}}$$\sqrt{1{-2x}^{2}}$dx=( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{8}$ | C. | $\frac{\sqrt{2}π}{4}$ | D. | $\frac{\sqrt{2}π}{8}$ |
13.已知函数f(x)=|cosx|•sinx,给出下列四个说法,其中正确说法是( )
| A. | 若|f(x1)|=|f(x2)|,则x1=x2+kπ(k∈Z) | B. | f(x)在区间$[-\frac{π}{4},\frac{π}{4}]$上单调递增 | ||
| C. | 函数f(x)的周期为π | D. | f(x)的图象关于点$(-\frac{π}{2},0)$成中心对称 |
10.若三角形ABC所在平面内一点M满足条件$\overrightarrow{CM}=\frac{1}{6}\overrightarrow{CB}+\frac{1}{3}\overrightarrow{CA}$,则S△MAC:S△MAB等于( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{6}$ |
9.下列说法正确的是( )
| A. | 命题“?x0∈R,x02+x0+2013>0”的否定是“?x∈R,x2+x+2013<0” | |
| B. | 命题p:函数f(x)=x2-2x仅有两个零点,则命题p是真命题 | |
| C. | 函数$f(x)=\frac{1}{x}$在其定义域上是减函数 | |
| D. | 给定命题p、q,若“p且q”是真命题,则?p是假命题 |
7.已知全集为R,集合A={x|($\frac{1}{2}$)x≤1},B={x|x≥2},A∩(∁RB)=( )
0 252525 252533 252539 252543 252549 252551 252555 252561 252563 252569 252575 252579 252581 252585 252591 252593 252599 252603 252605 252609 252611 252615 252617 252619 252620 252621 252623 252624 252625 252627 252629 252633 252635 252639 252641 252645 252651 252653 252659 252663 252665 252669 252675 252681 252683 252689 252693 252695 252701 252705 252711 252719 266669
| A. | [0,2) | B. | [0,2] | C. | (1,2) | D. | (1,2] |
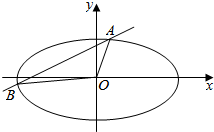 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,短轴的一个顶点与椭圆两焦点构成的三角形面积为2$\sqrt{3}$.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,短轴的一个顶点与椭圆两焦点构成的三角形面积为2$\sqrt{3}$.