题目内容
16.kx2-kx+2>0恒成立,则k的取值范围是[0,8).分析 讨论k是否为0,当k不等于0时,根据判别式与系数的关系得到不等式恒成立的等价条件.
解答 解:①k=0时,不等式为2>0恒成立,故满足题意;
②k≠0时,x∈R时,kx2-kx+2>0恒成立,
等价于$\left\{\begin{array}{l}{k>0}\\{△{=k}^{2}-8k<0}\end{array}\right.$,解得0<k<8;
综上x∈R时,kx2-kx+2>0恒成立,
k的取值范围是0≤k<8;
故答案为:[0,8).
点评 本题考查了一元二次不等式恒成立时求参数范围;首先要考虑二次项系数是否为0,然后根据判别式与系数的关系得到关于k的不等式解之.

练习册系列答案
相关题目
4.要得到函数y=3sin(2x+$\frac{π}{3}$)的图象,只需将y=3sin2x图象上所有的点( )
| A. | 向左平行移动$\frac{π}{3}$个单位长度 | B. | 向右平行移动$\frac{π}{3}$个单位长度 | ||
| C. | 向左平行移动$\frac{π}{6}$个单位长度 | D. | 向右平行移动$\frac{π}{6}$个单位长度 |
6.如果执行如图的程序框图,那么输出的值是( )
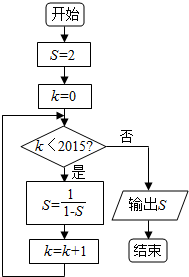

| A. | 2015 | B. | -1 | C. | $\frac{1}{2}$ | D. | 2 |
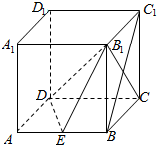 如图,在正方体ABCD-A1B1C1D1的棱长为a,E为棱AB上的一动点.
如图,在正方体ABCD-A1B1C1D1的棱长为a,E为棱AB上的一动点.