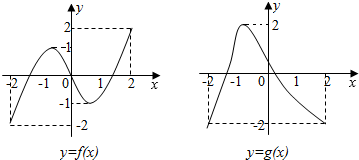20.对于给定的正数K,定义函${f_K}(x)=\left\{\begin{array}{l}f(x),f(x)≤K\\ K,f(x)>K\end{array}\right.$.已知函数$f(x)={(\frac{1}{3})^{{x^2}-4x}}(0≤x<5)$,对其定义域内的任意x,恒有fk(x)=f(x),则( )
| A. | K的最小值为$\frac{1}{243}$ | B. | K的最大值为$\frac{1}{243}$ | C. | K的最小值为81 | D. | K的最大值为81 |
19.若x∈R,n∈N*,规定:$H_x^n=x(x+1)(x+2)…(x+n-1)$,例如:$H_{-4}^4=(-4)•(-3)•(-2)•(-1)=24$,则函数$f(x)=x•H_{x-1}^3$的图象( )
| A. | 关于原点对称 | B. | 关于直线y=x对称 | C. | 关于x轴对称 | D. | 关于y轴对称 |
18.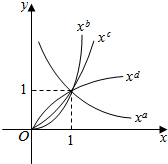 幂函数y=xa,y=xb,y=xc,y=xd在第一象限的图象如图所示,则a,b,c,d的大小关系是 ( )
幂函数y=xa,y=xb,y=xc,y=xd在第一象限的图象如图所示,则a,b,c,d的大小关系是 ( )
 幂函数y=xa,y=xb,y=xc,y=xd在第一象限的图象如图所示,则a,b,c,d的大小关系是 ( )
幂函数y=xa,y=xb,y=xc,y=xd在第一象限的图象如图所示,则a,b,c,d的大小关系是 ( )| A. | a>b>c>d | B. | d>b>c>a | C. | d>c>b>a | D. | b>c>d>a |
15.给定函数①$y={x^{\frac{1}{2}}}$,②$y=x+\frac{1}{x}$,③y=|x-1|,④y=2x+1,其中在区间(0,1)上单调递减的函数序号是( )
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
14.已知下列命题
①b2=ac,则a,b,c成等比数列;
②若{an}为等差数列,且常数c>0,则数列{can}为等比数列;
③若{an}为等比数列,且常数c>0,则数列{can}为等比数列;
④常数列既为等差数列,又是等比数列.
其中,真命题的个数为( )
0 252342 252350 252356 252360 252366 252368 252372 252378 252380 252386 252392 252396 252398 252402 252408 252410 252416 252420 252422 252426 252428 252432 252434 252436 252437 252438 252440 252441 252442 252444 252446 252450 252452 252456 252458 252462 252468 252470 252476 252480 252482 252486 252492 252498 252500 252506 252510 252512 252518 252522 252528 252536 266669
①b2=ac,则a,b,c成等比数列;
②若{an}为等差数列,且常数c>0,则数列{can}为等比数列;
③若{an}为等比数列,且常数c>0,则数列{can}为等比数列;
④常数列既为等差数列,又是等比数列.
其中,真命题的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |